





The originator of the office webcam dropped by my office today. He was here to give a guest talk about the Kauffman bracket.
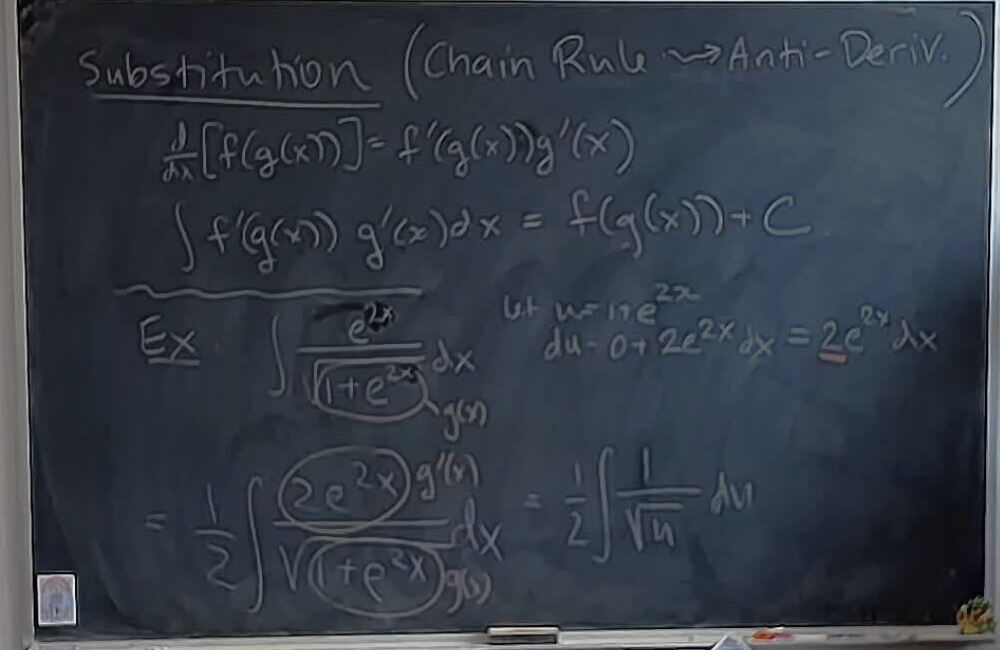

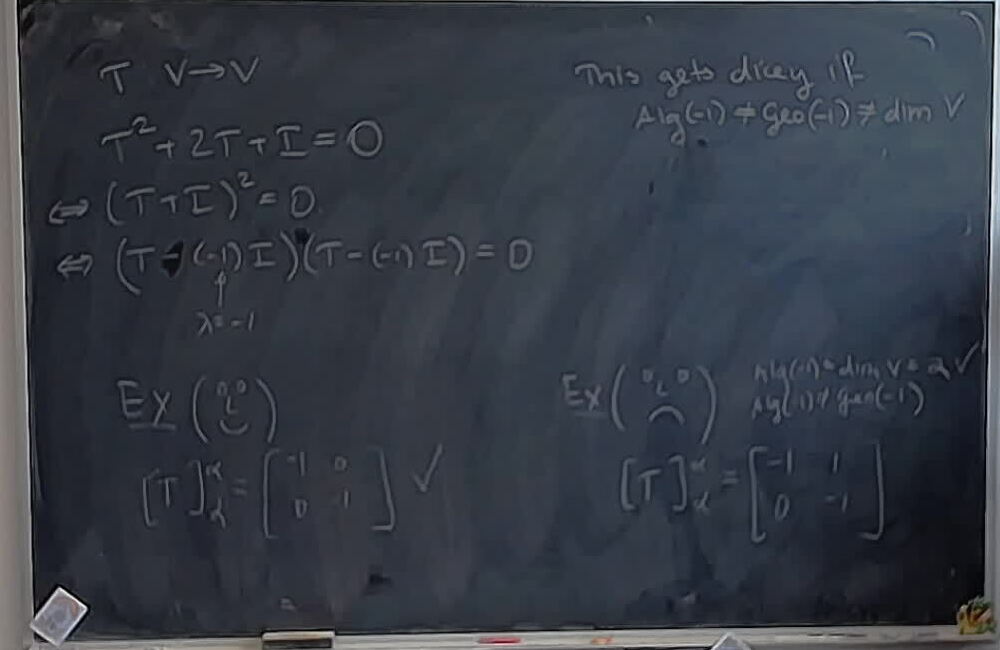
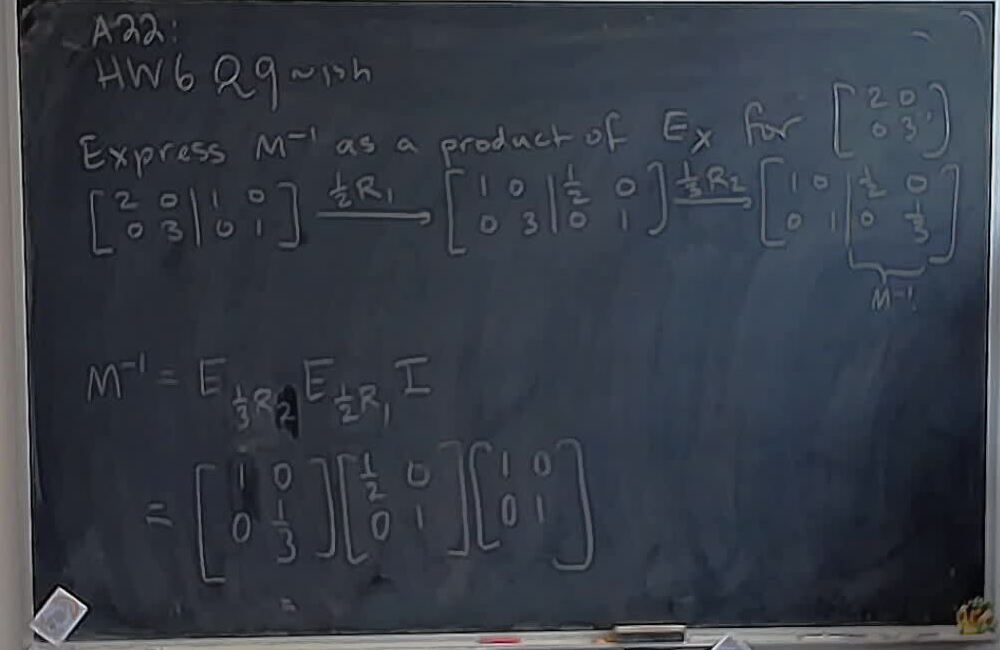
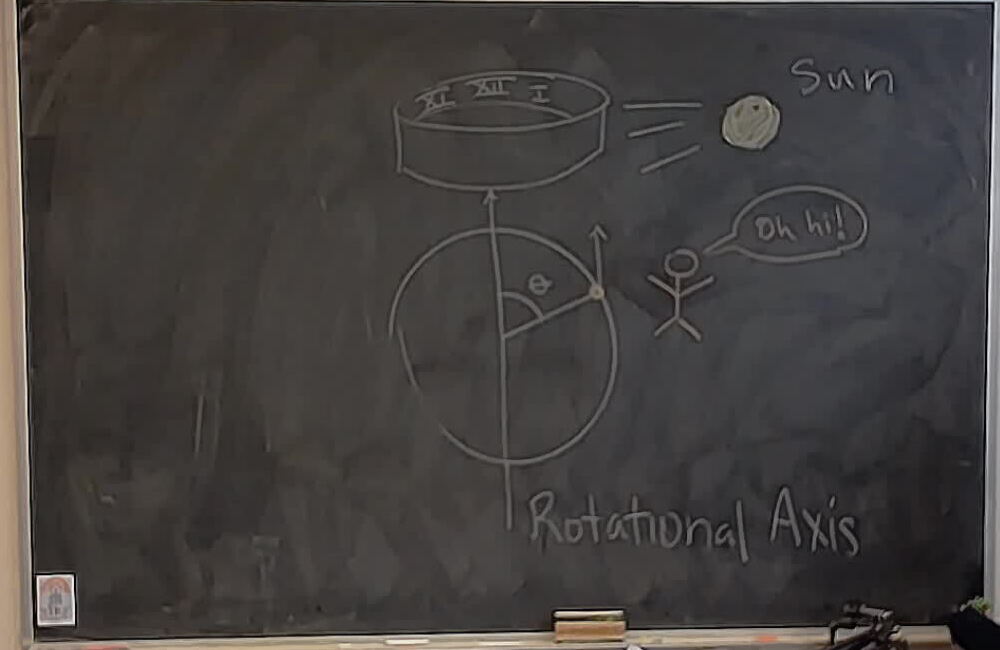
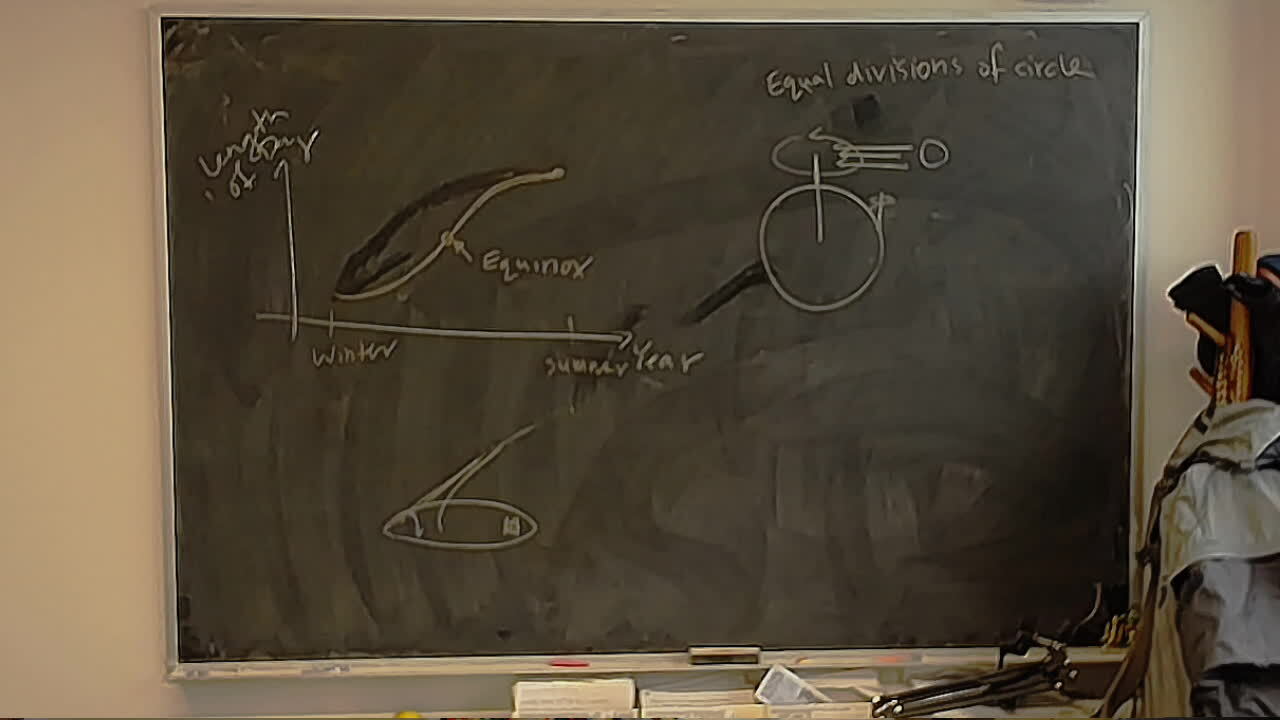
A sketch for a piece about sundials. This shows the first step in designing an equitorial dial.
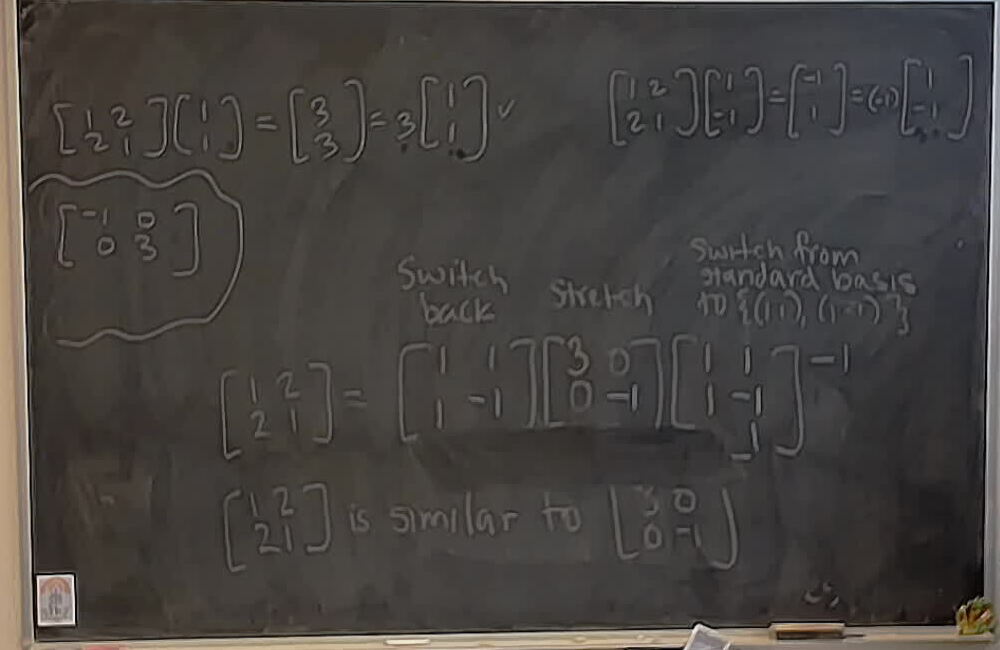
Diagonalizing the matrix: \[ \begin{bmatrix} 1 & 2\ 2 & 1 \end{bmatrix} \]
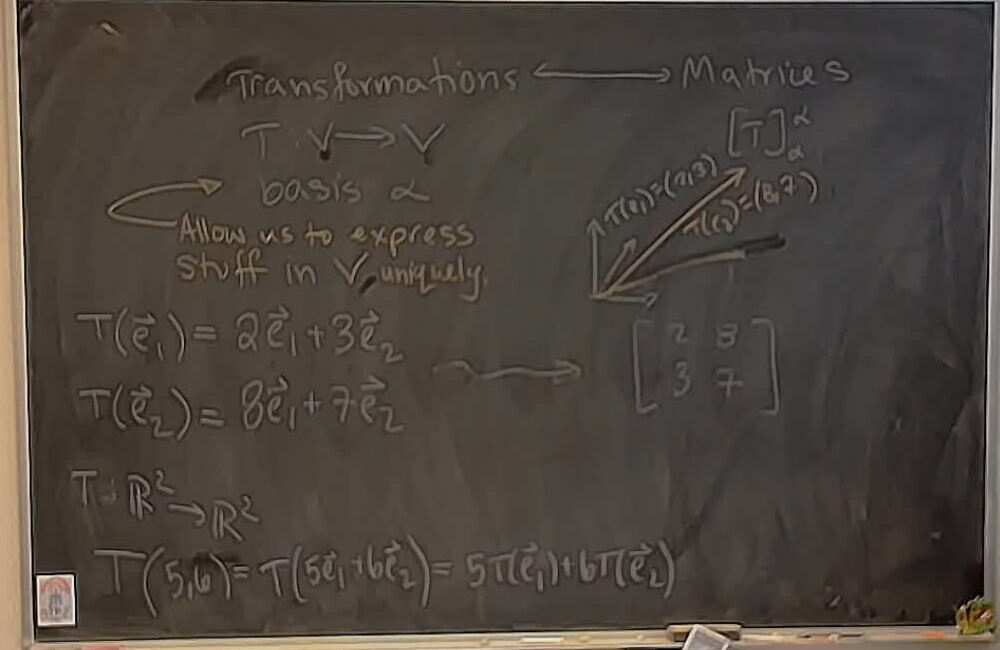

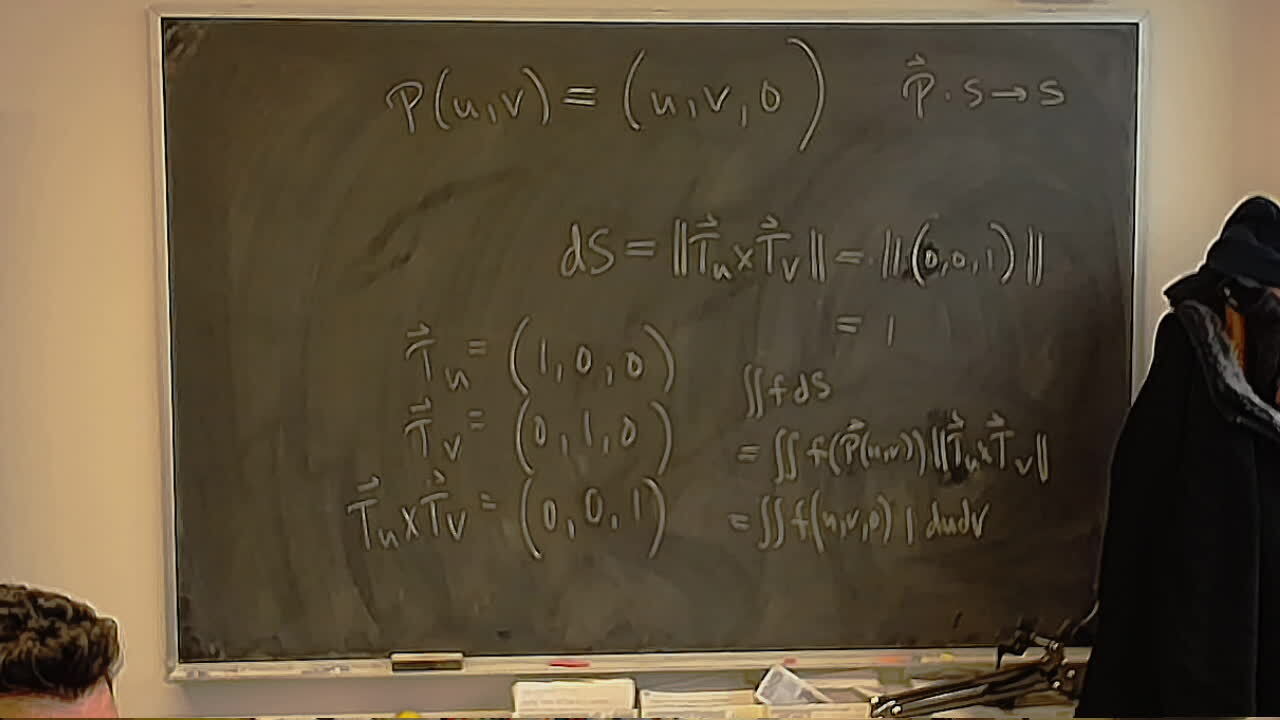



There is a webcam in my office that I use to take photos of the whiteboard. This setup was inspired by Dror Bar Natan’s Blackboard Shots. If you know of anyone else with a similar setup, please let me know.




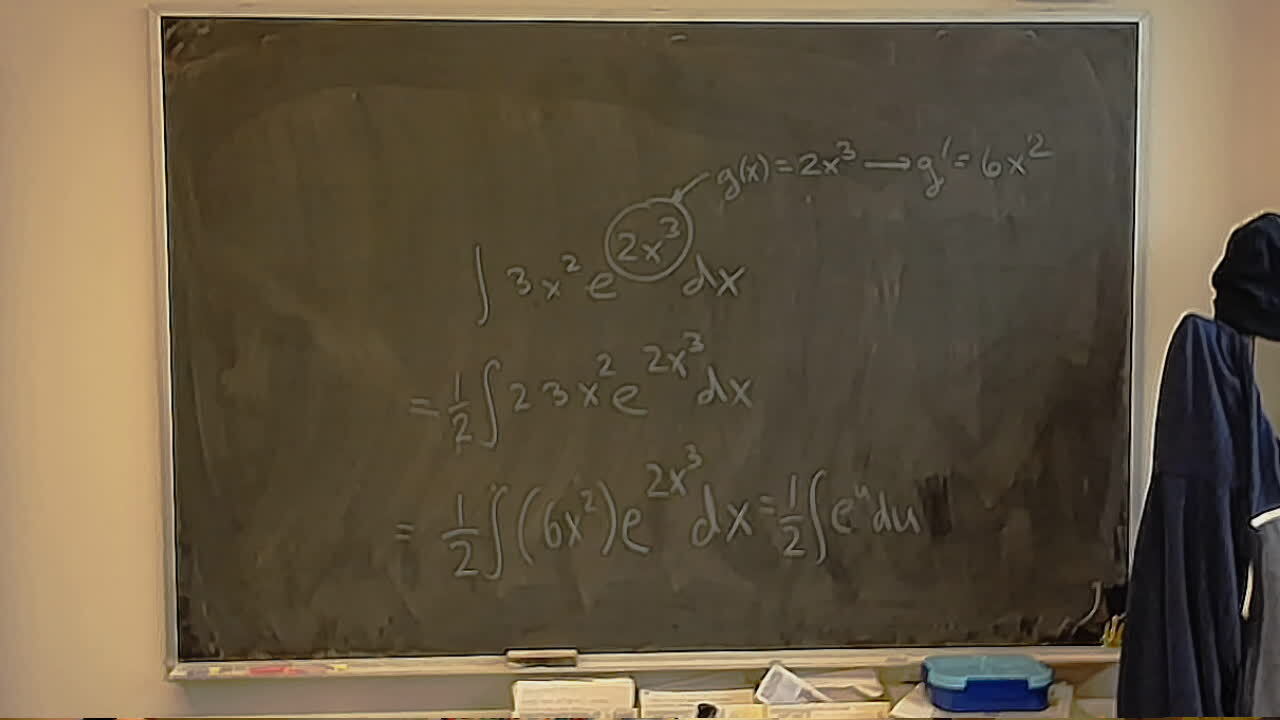
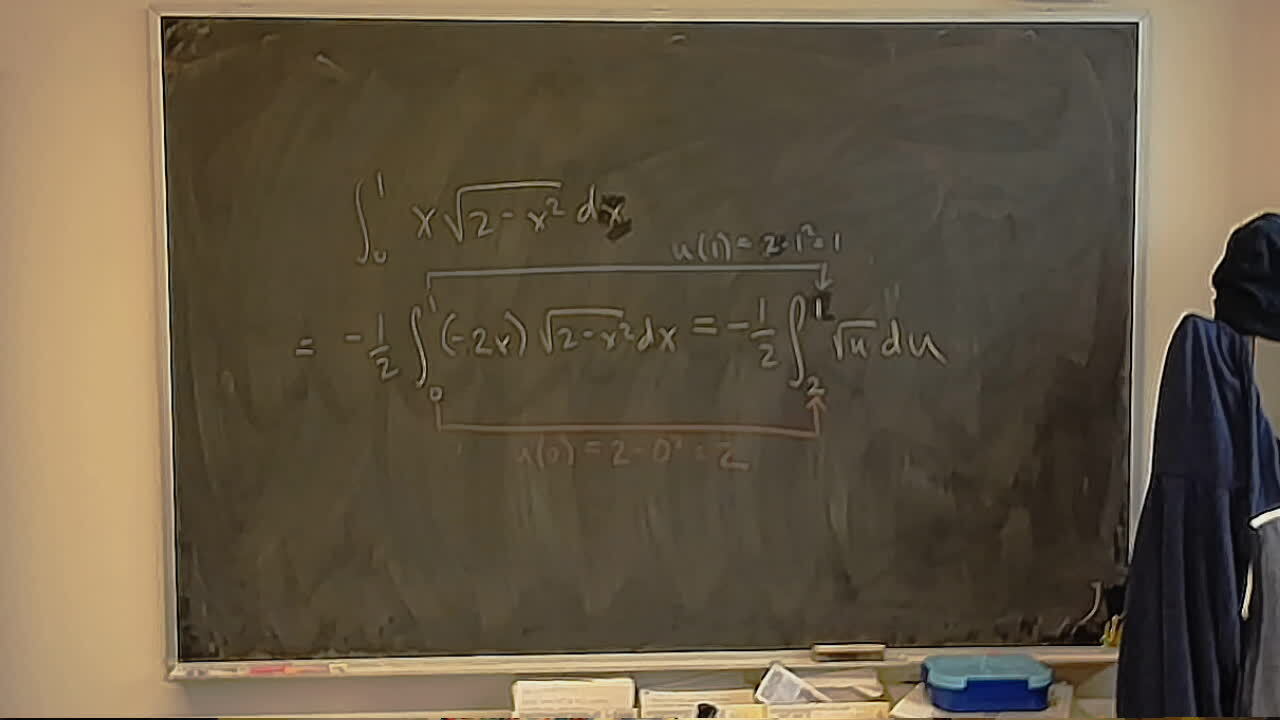
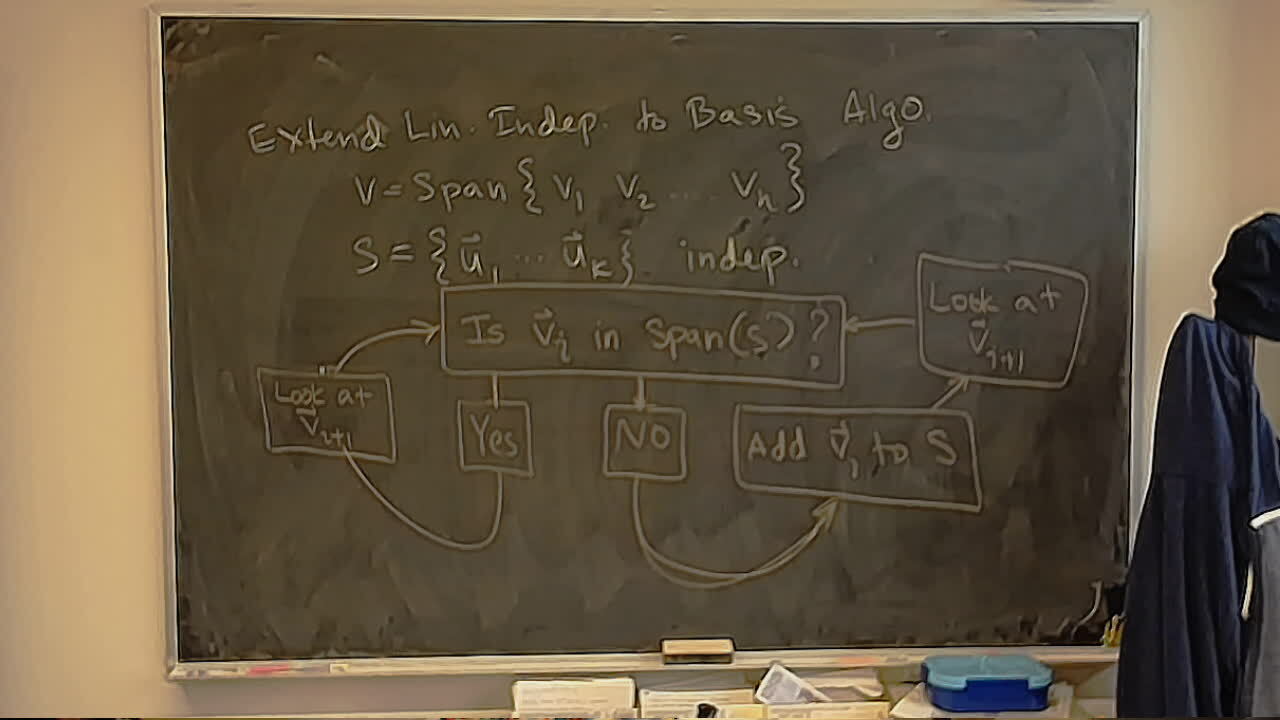
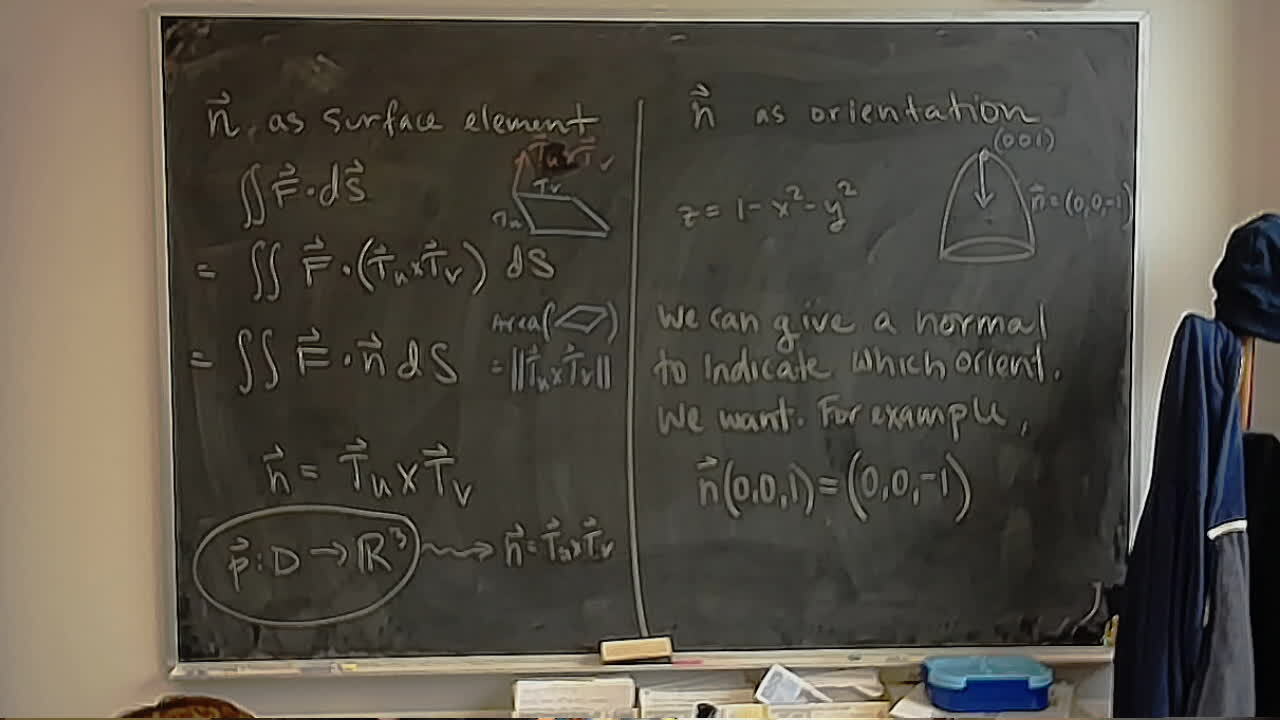
Divy wanted to come in and see the World Famous Office Camera.
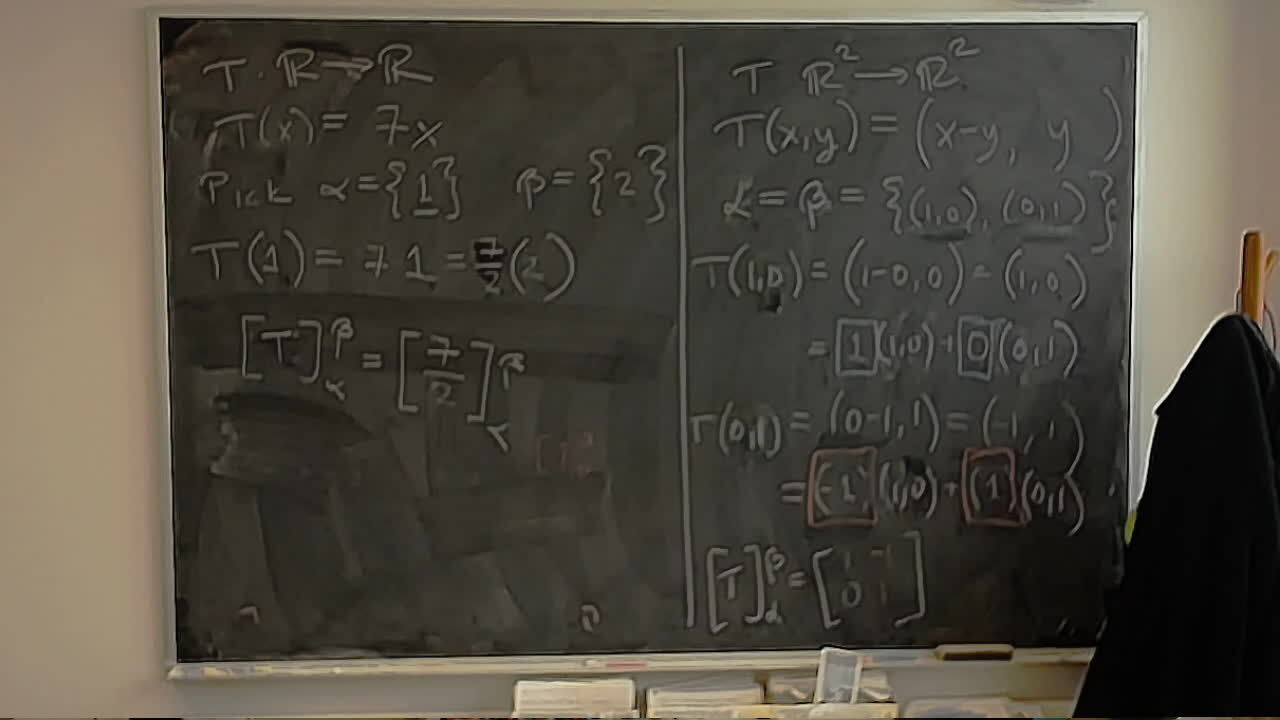
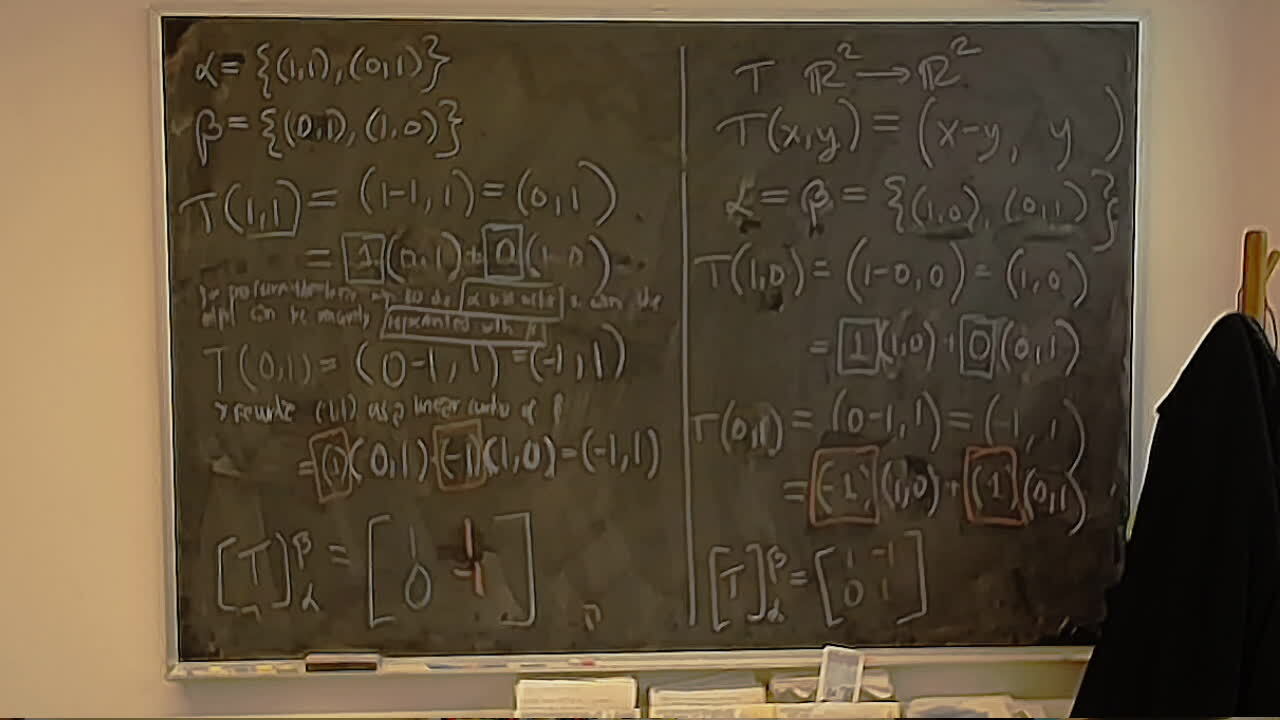
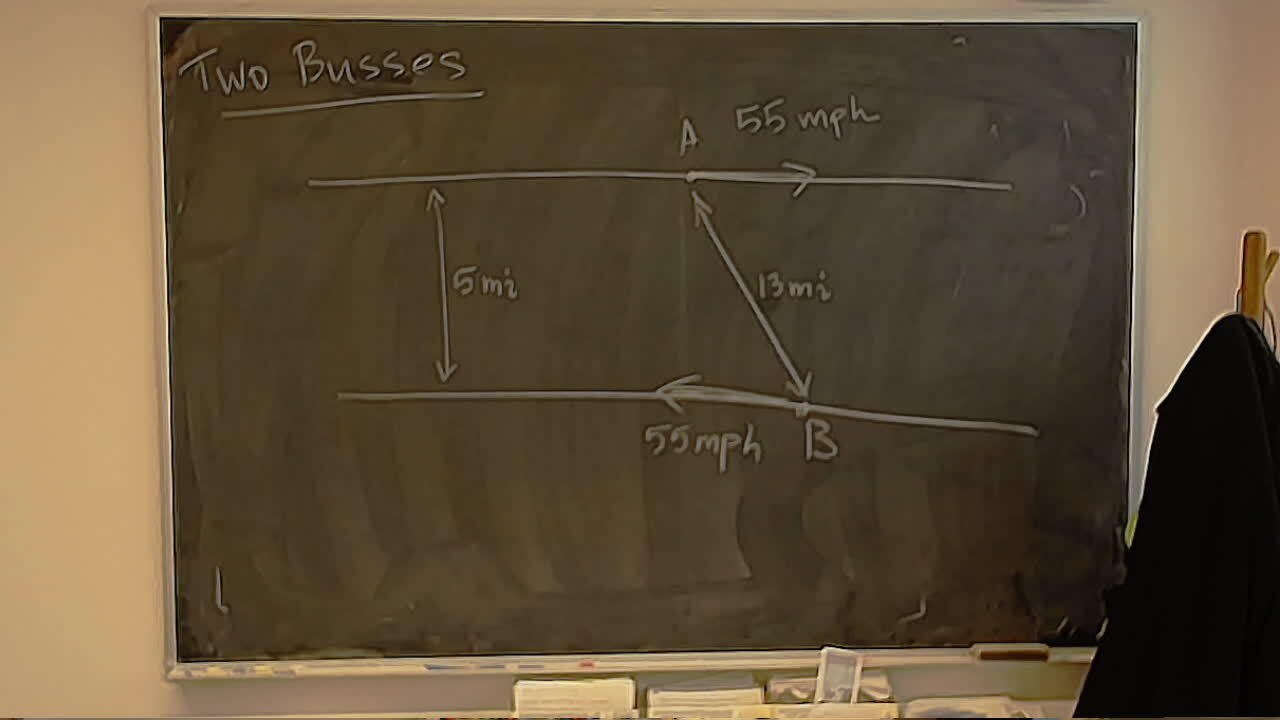
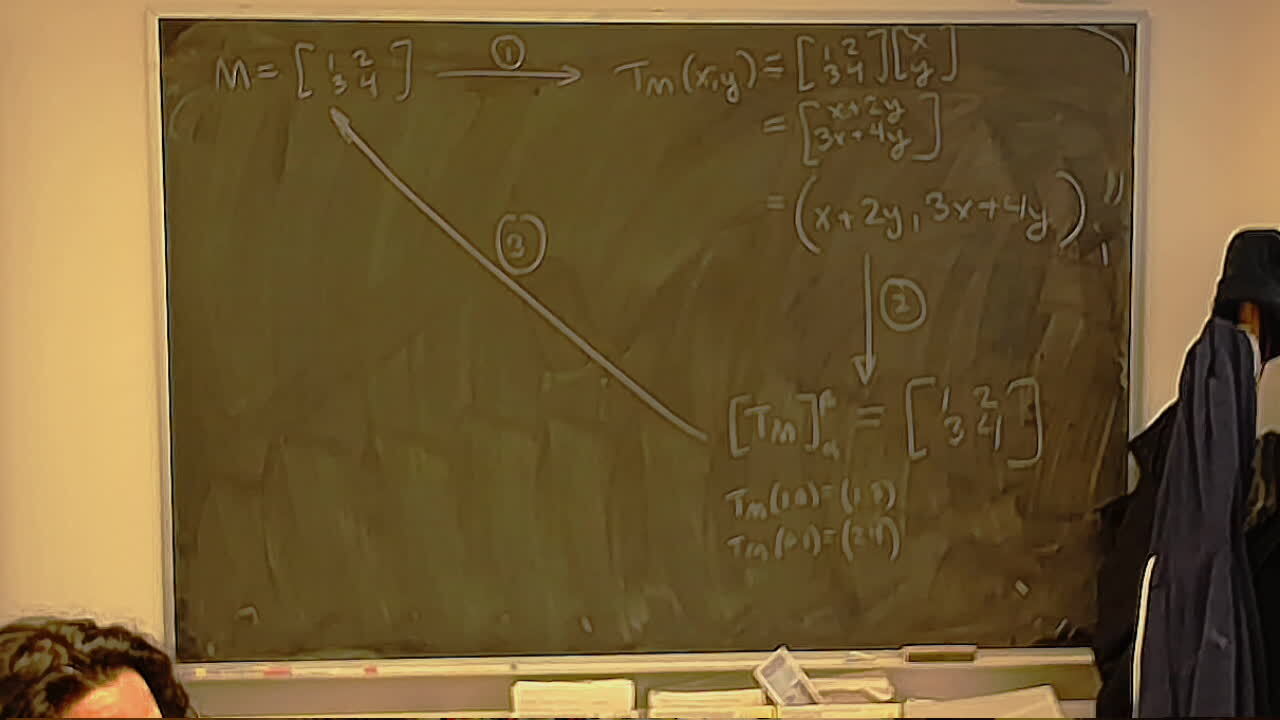
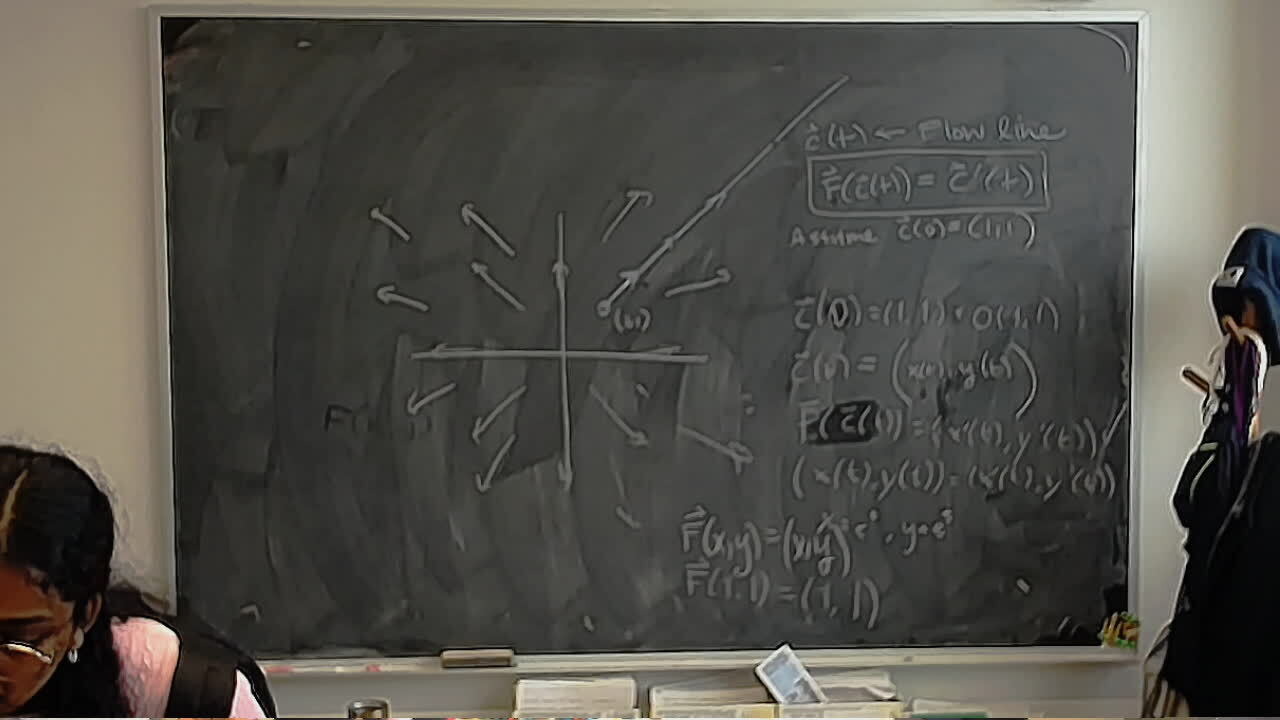

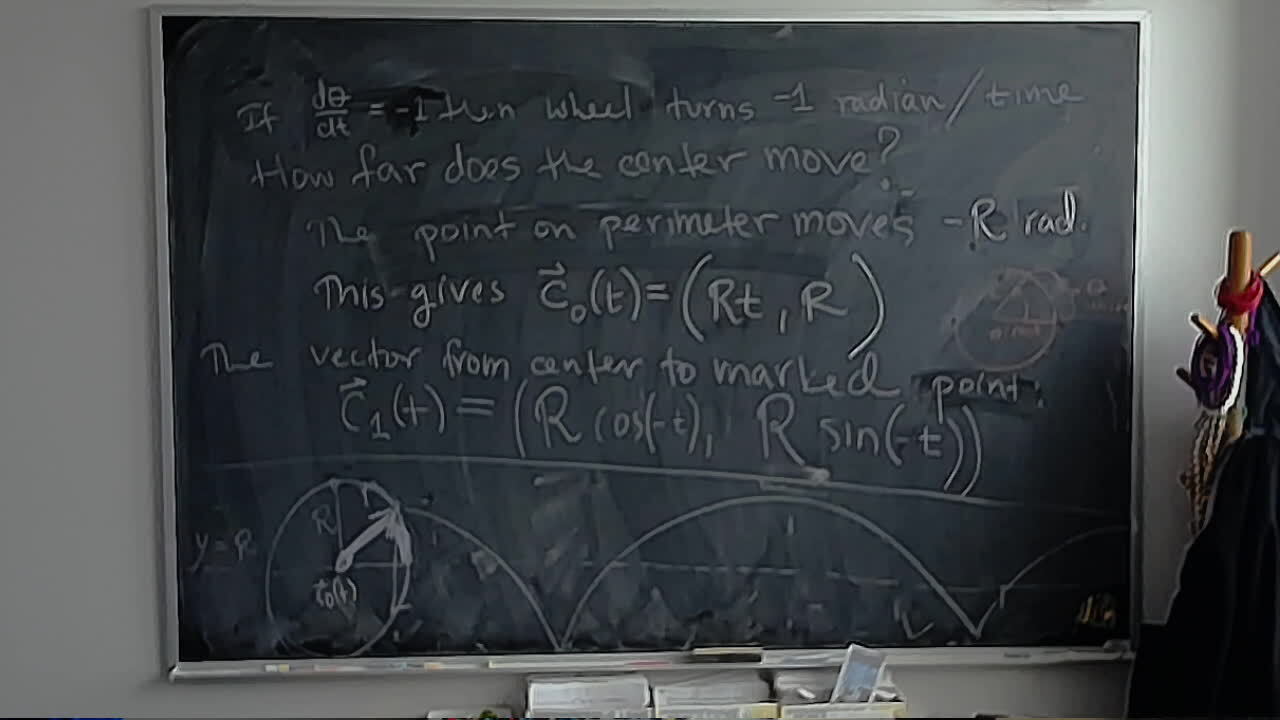



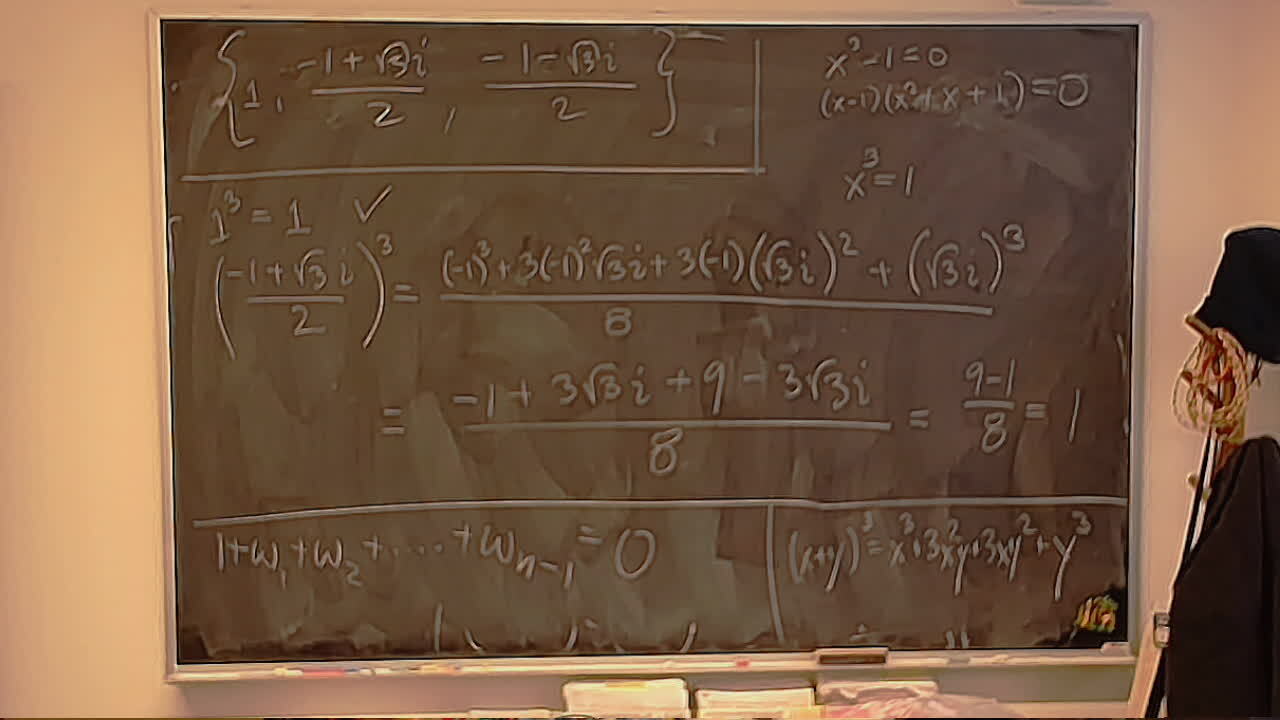

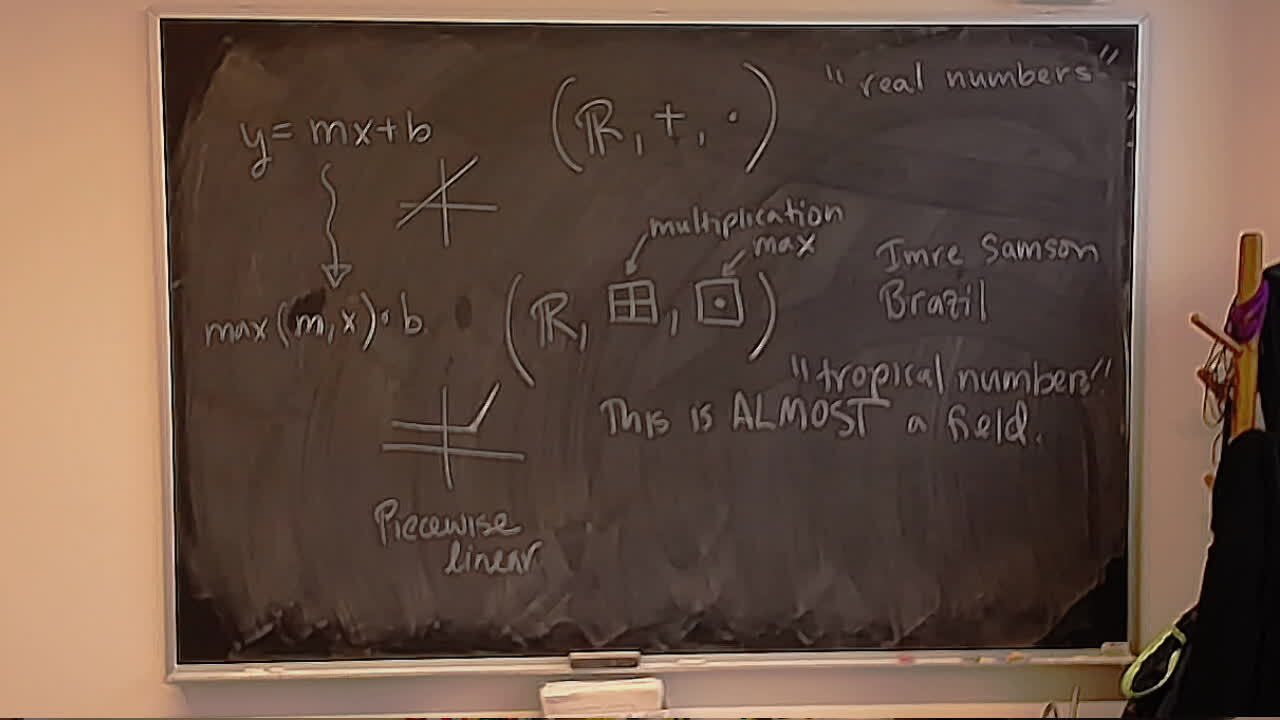
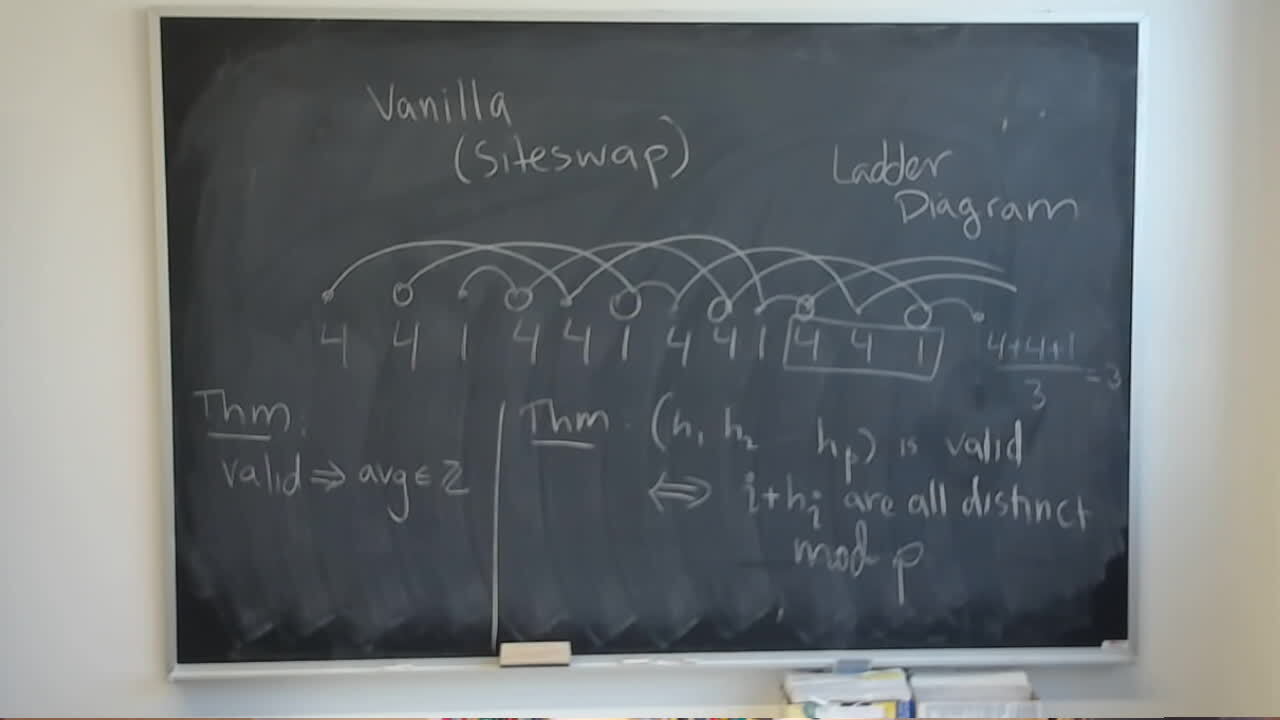
Converting a calculation from Storer’s Heart Sequences to the Heart Group
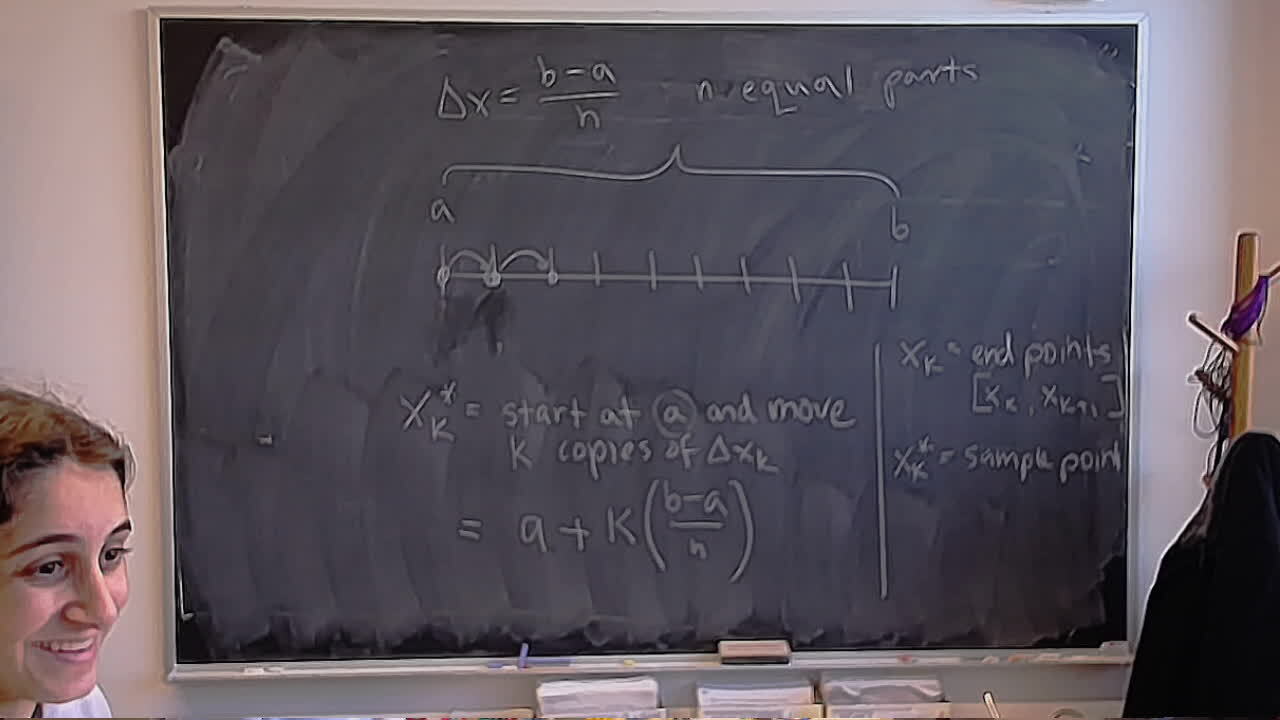
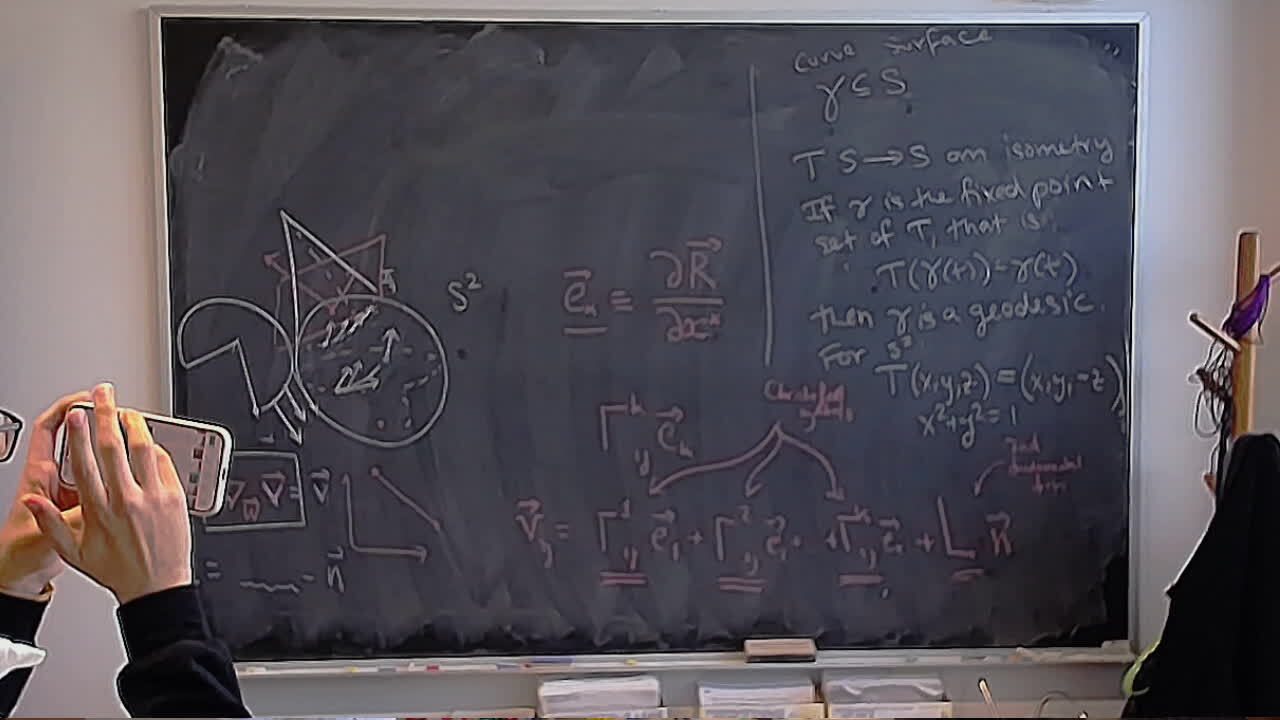
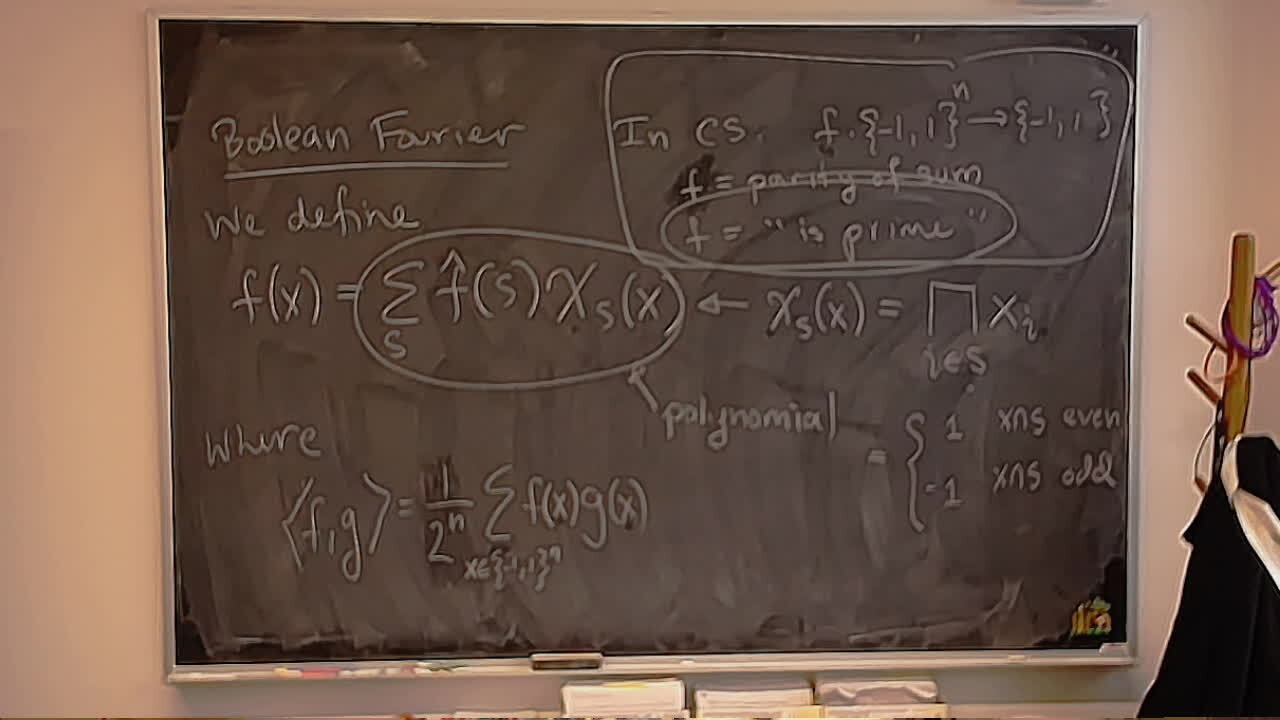
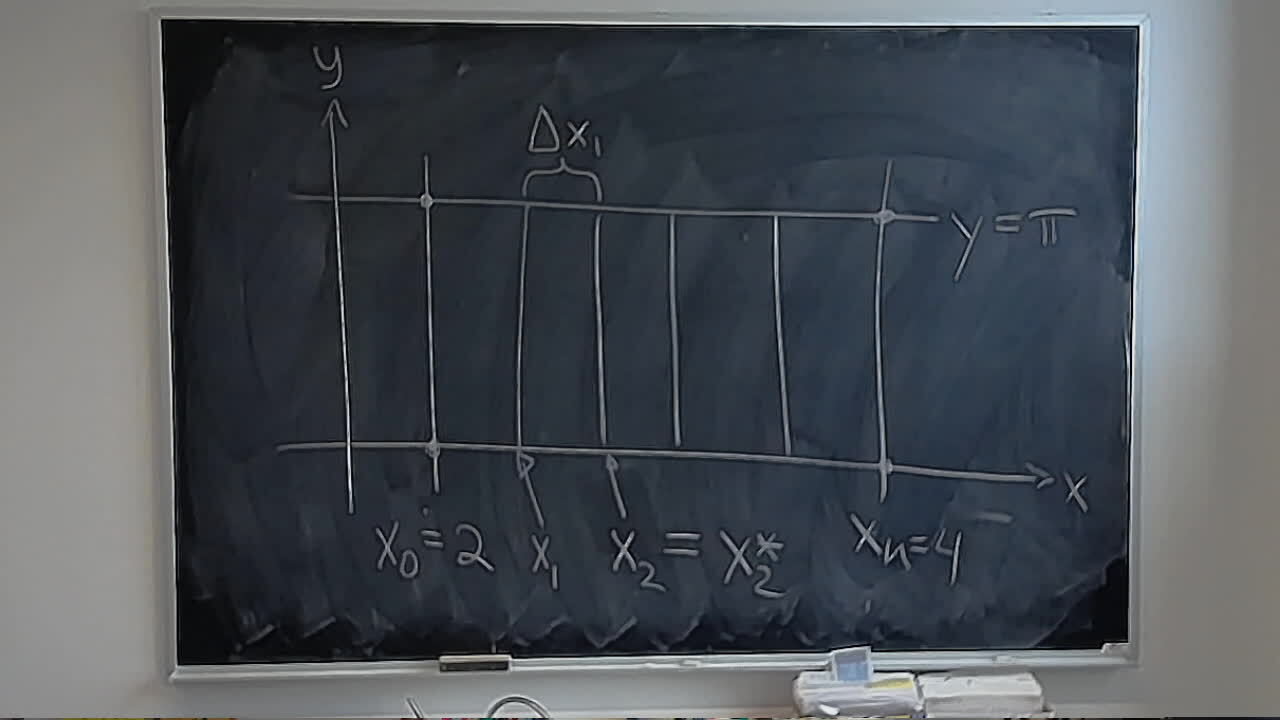
A happy welcome back after a long break.


My colleague Nick Cheng asked about the curve $f(p) = x^p - x$ for $x \in (0,1)$ and $p \in (0,1)$. He was interested in where the maximum is for various values of $p$.


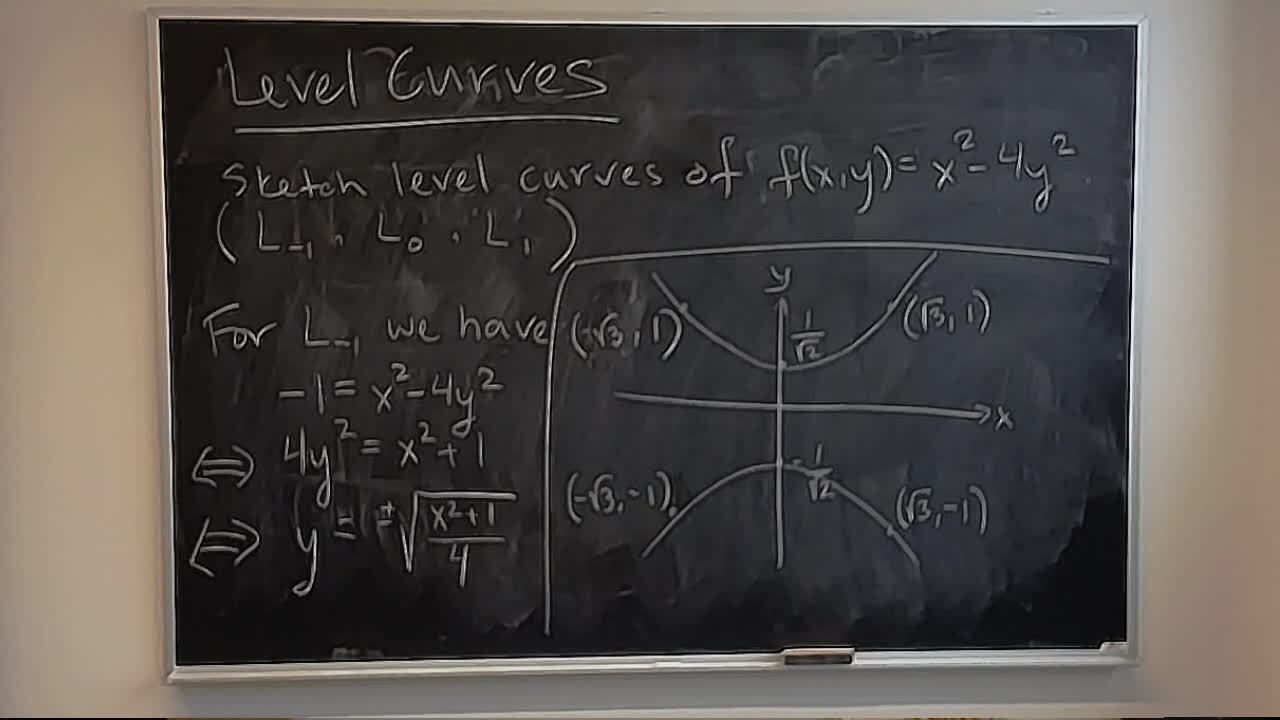
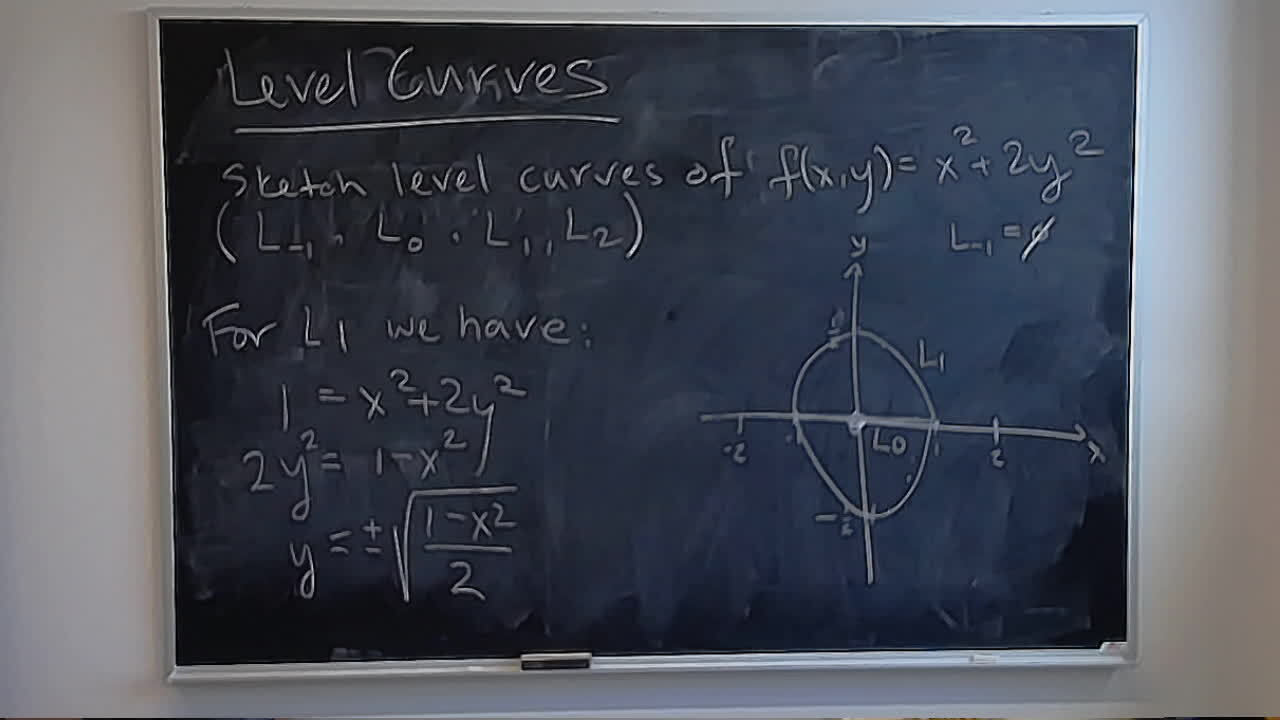
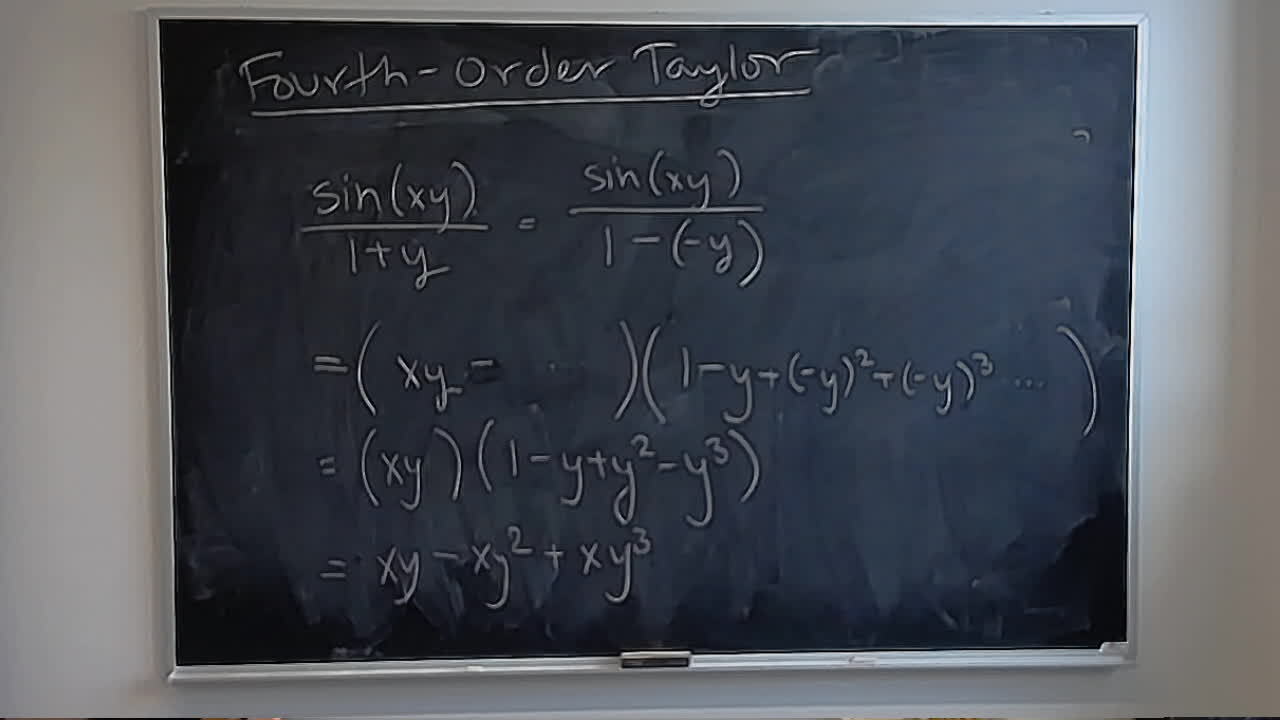

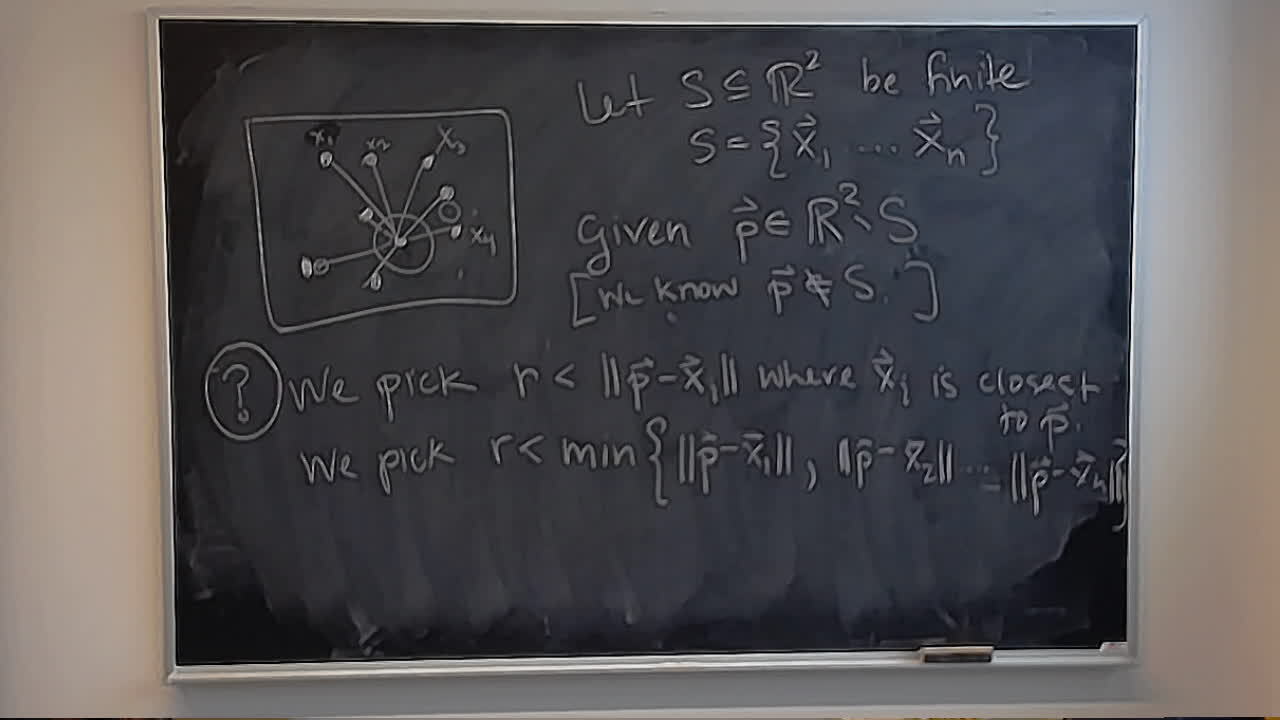



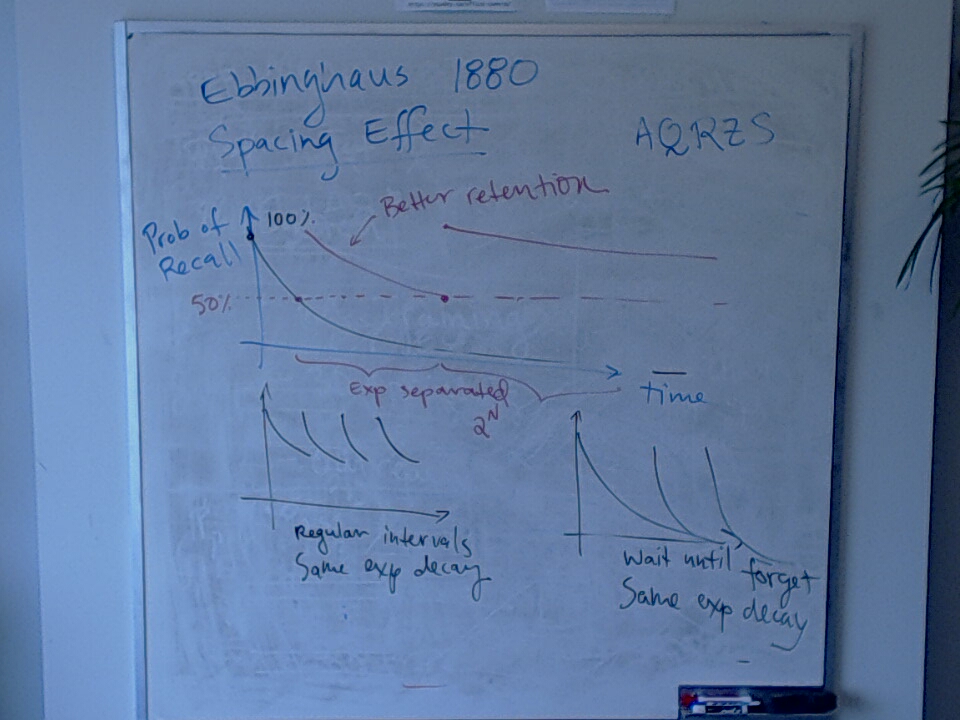
Here is a wonderful interactive essay about the spacing effect: How to Remember Anything Forever~ish.
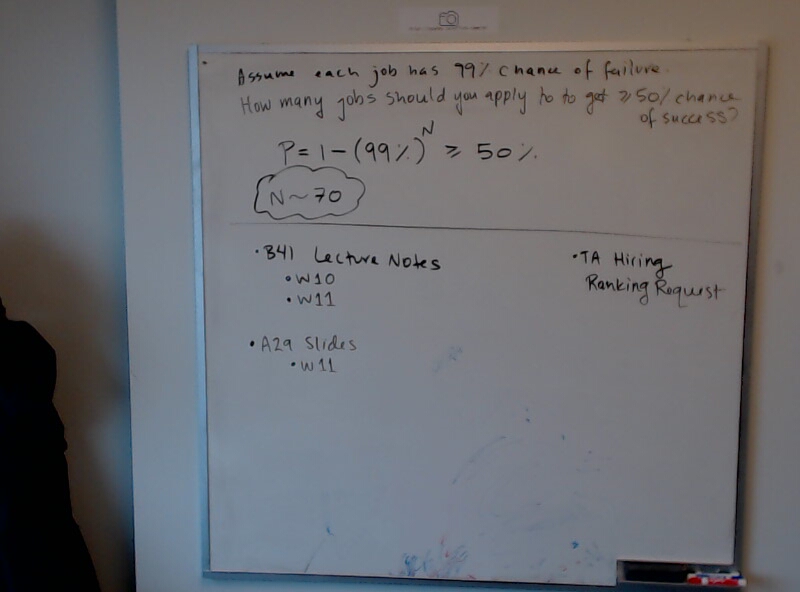
This is $ \LaTeX $.

This is my friend Alex Teeter, manifold explorer.

 This is my friend, Paco Estrada.
This is my friend, Paco Estrada.
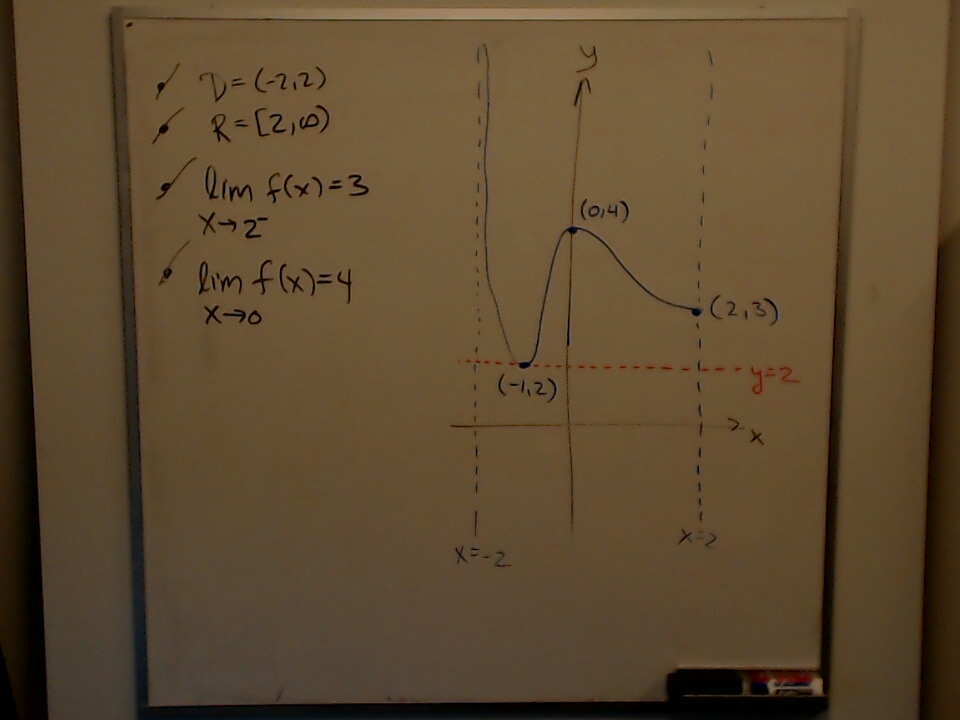
The designer graph on the first term test for MAT A29 Winter 2022.

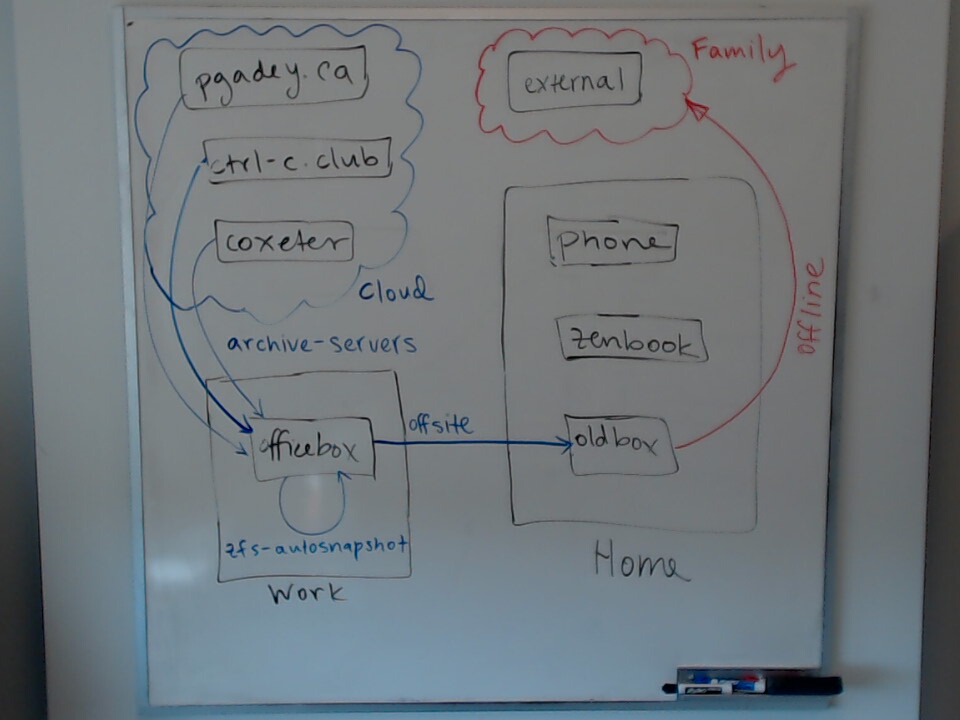
This is the current layout of my Backup System.
It shows how: archive-servers.sh, offline-backup.sh, and offsite-backup.sh work.
The Syncthing and Tailscale connections are not shown for the sake of clarity.












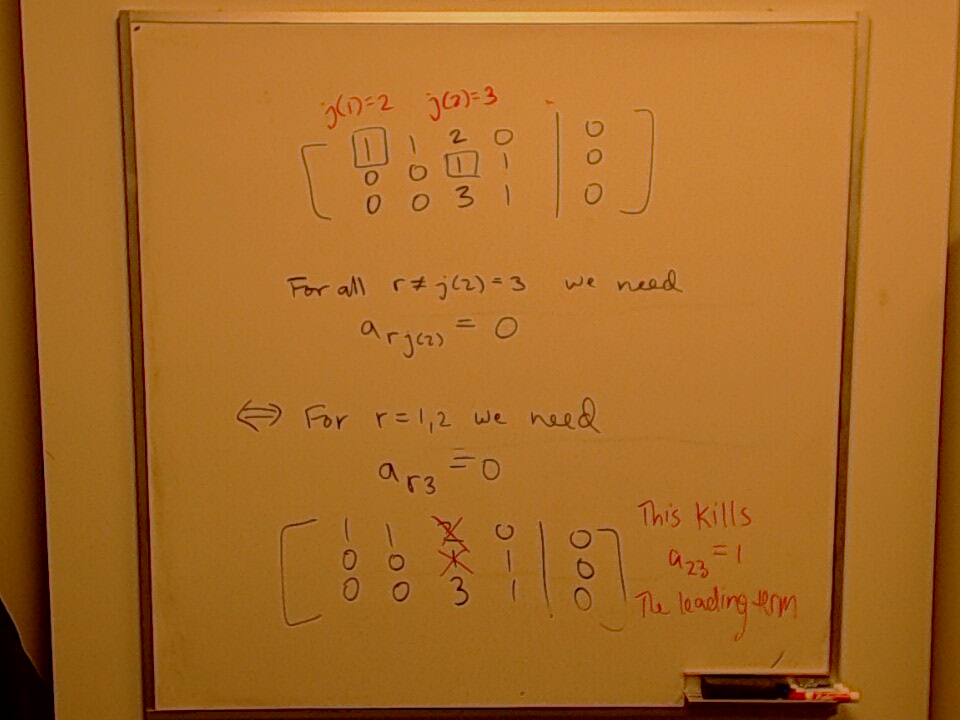










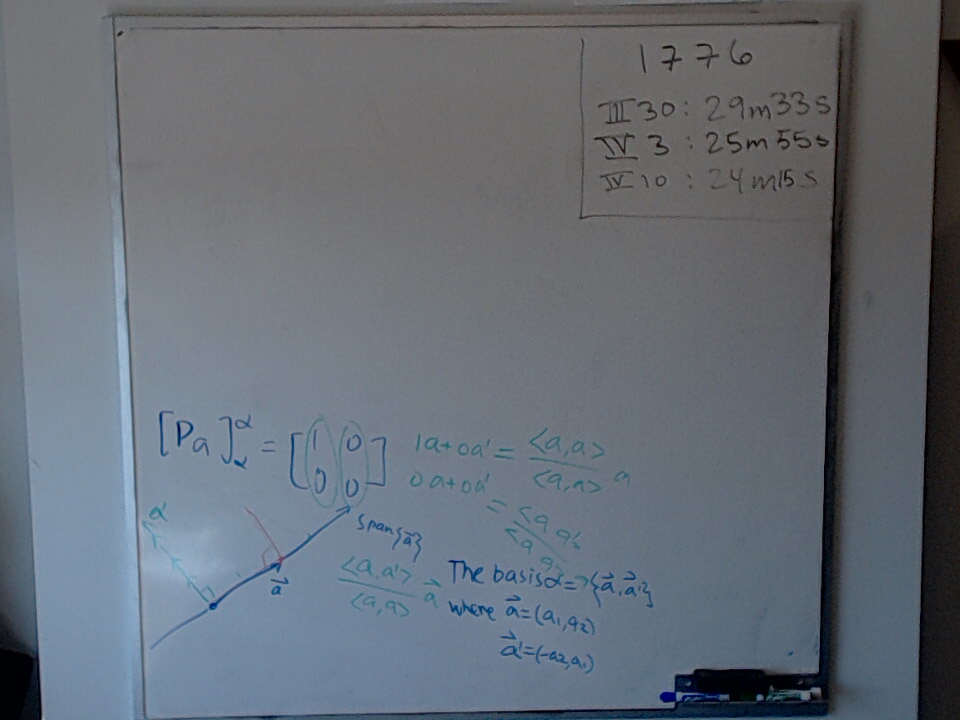
We find a linear system with solution set $\operatorname{Span}({ (1,0,2,3), (0,1,4,5)})$.


























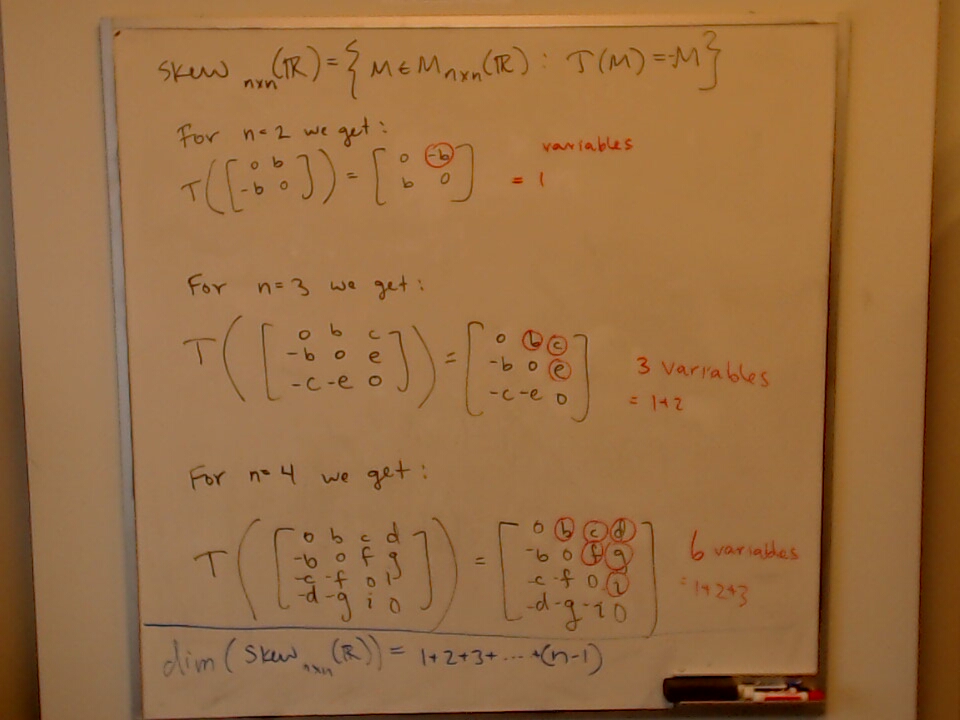


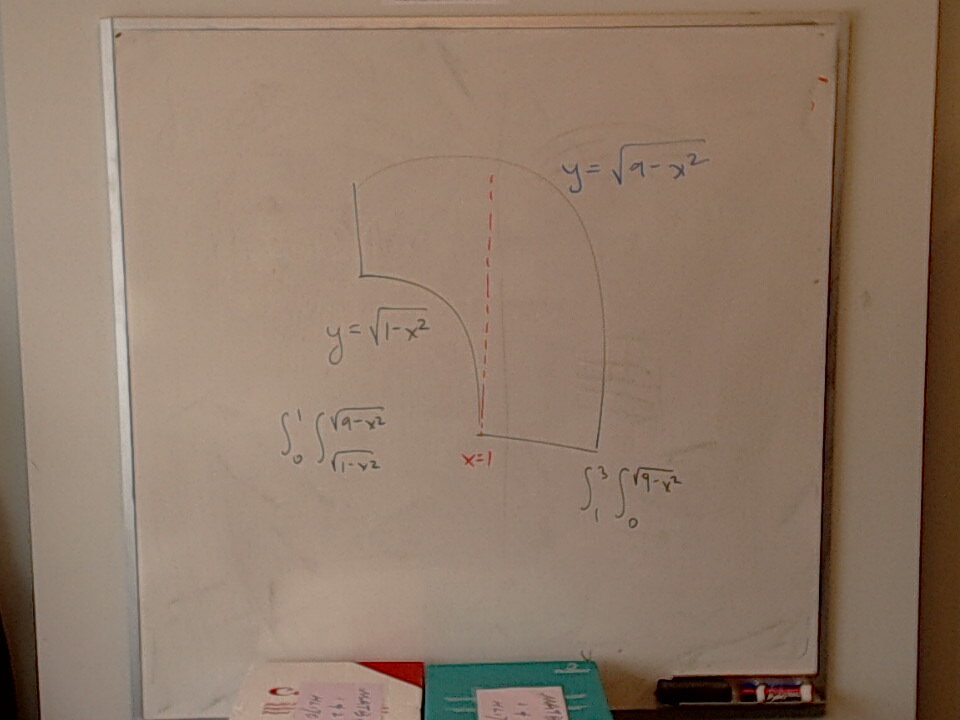


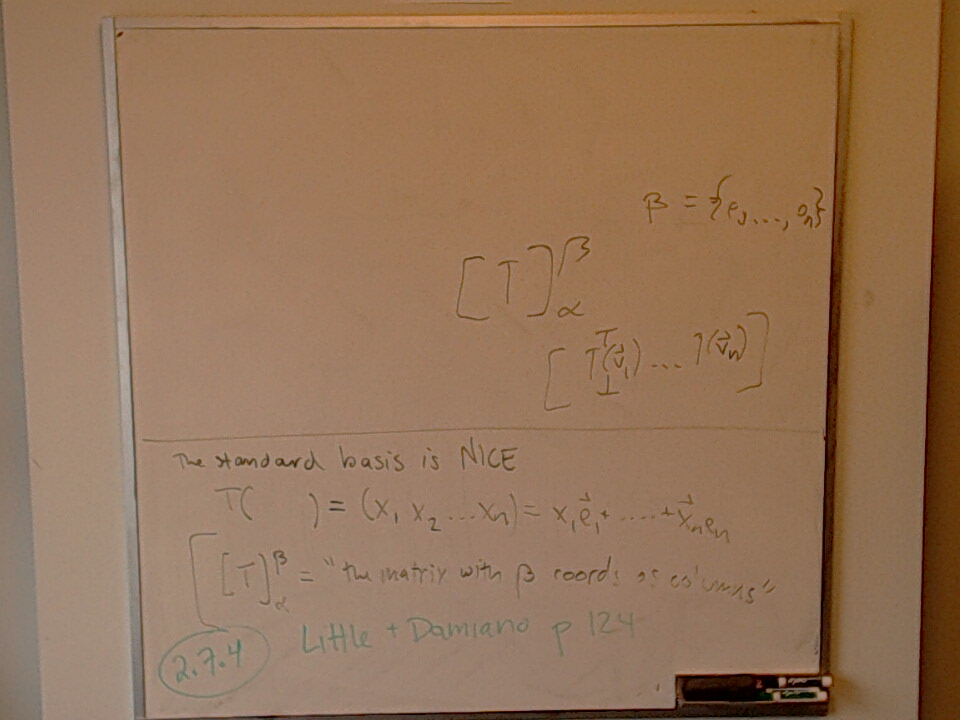








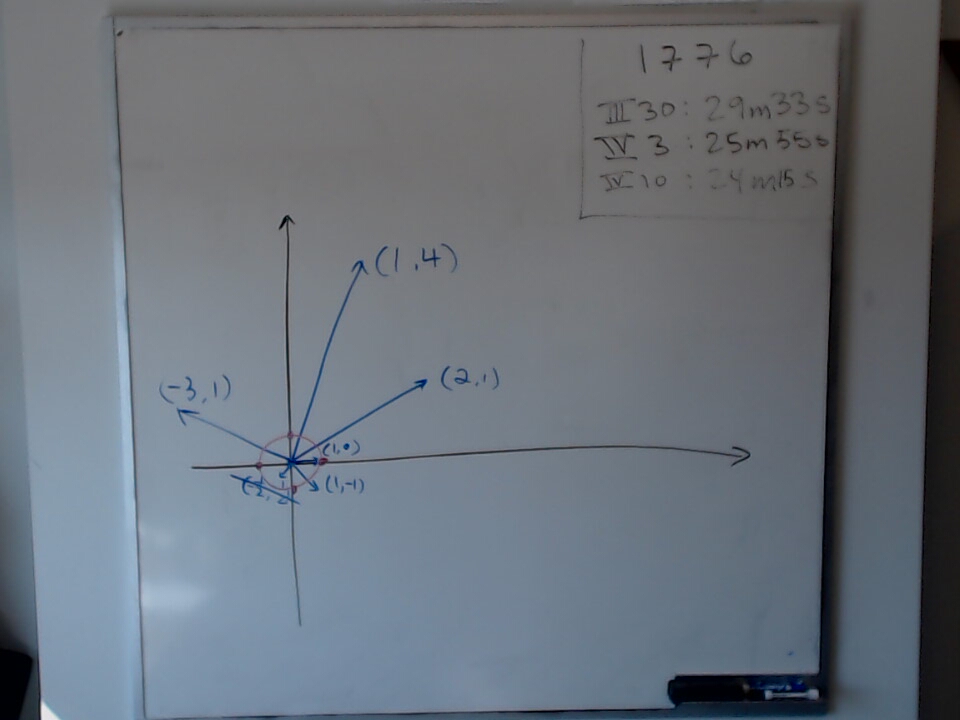












My daughter Mira came in to the office this afternoon and coloured.

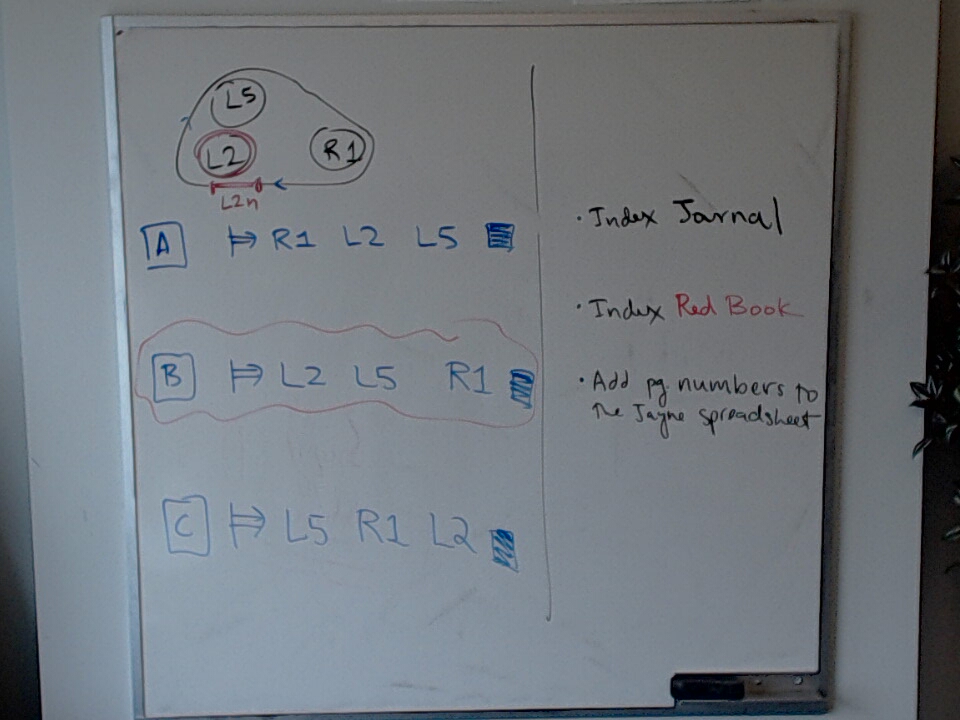
The canonical start of a linear sequence is a point in nearest LFn string. In this simple example, there are three possible linear sequences (with the correct orientation) but only $L2, L5, R1$ has the correct start point.


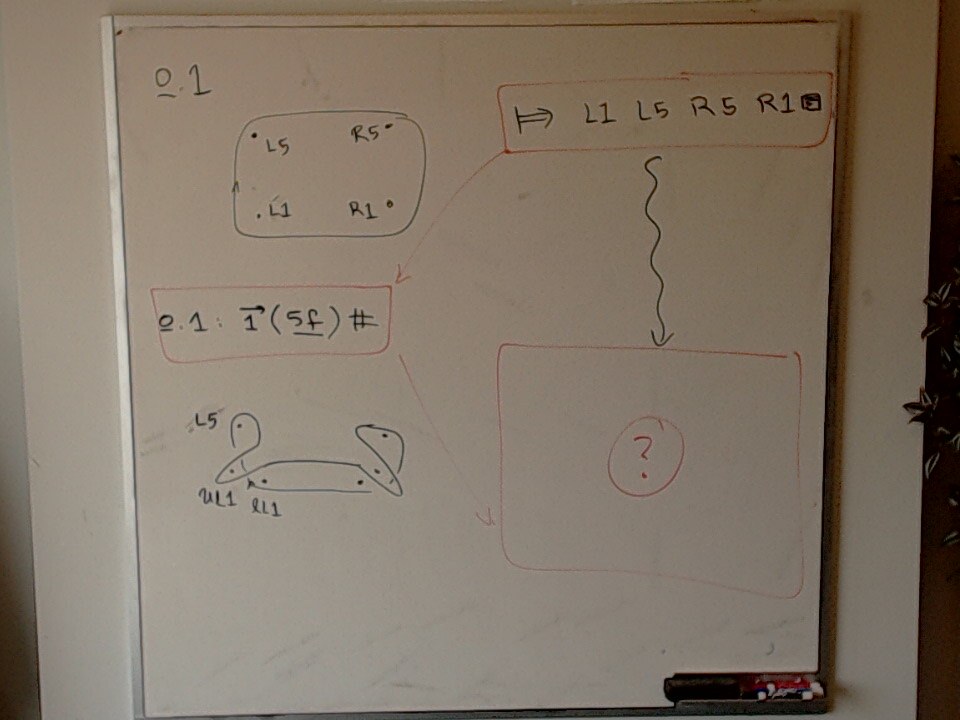

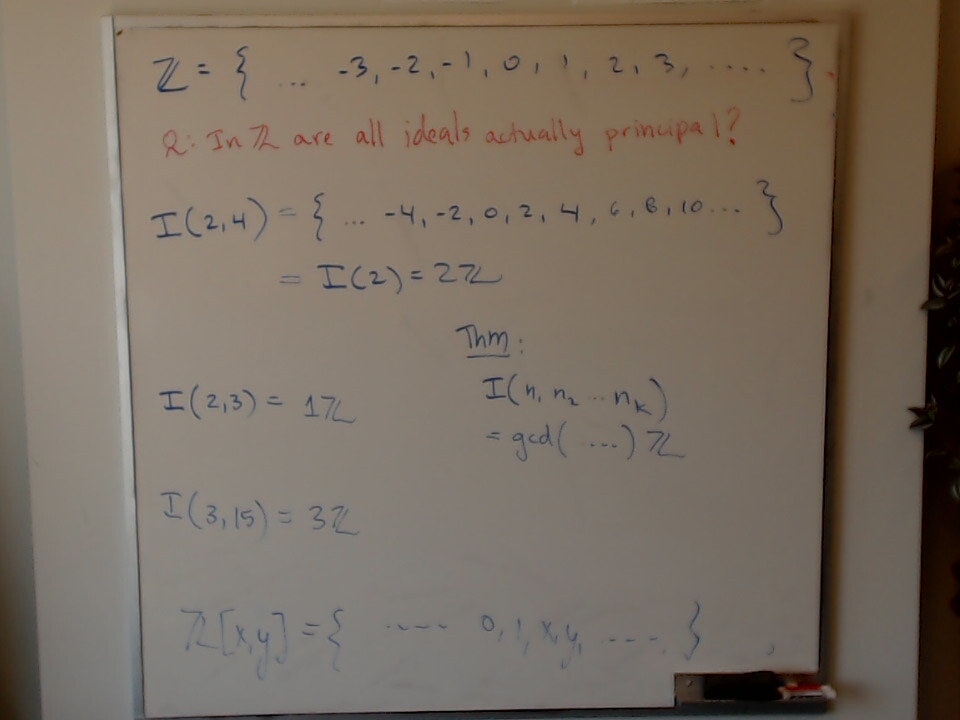
![Ideals and Principal Ideals: Are all ideals in Z[x,y] actually principal? A photo of a whiteboard titled: Ideals and Principal Ideals: Are all ideals in Z[x,y] actually principal?](/images/office-camera/2023-05-30T12:01:54-04:00.jpeg)




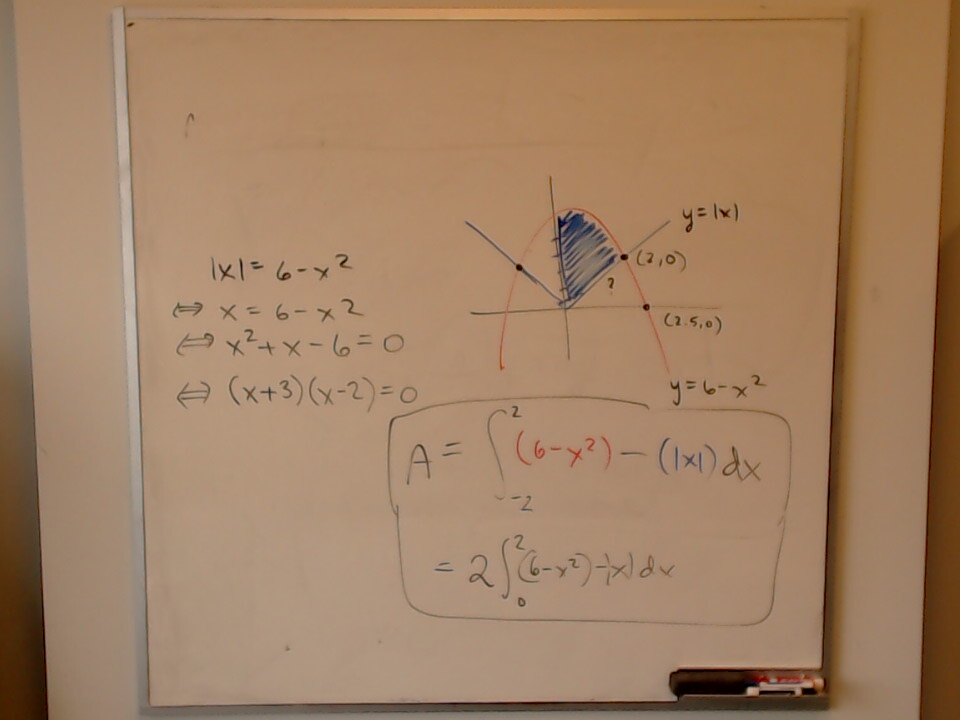
For positive integers $m$ and $n$, let $f(m, n)$ denote the number of $n$-tuples $(x_1, x_2, \dots , x_n)$ of integers such that $|x_1|+|x_2|+ \cdots +|x_n| \leq m$. Show that $f(m, n) = f(n, m)$.







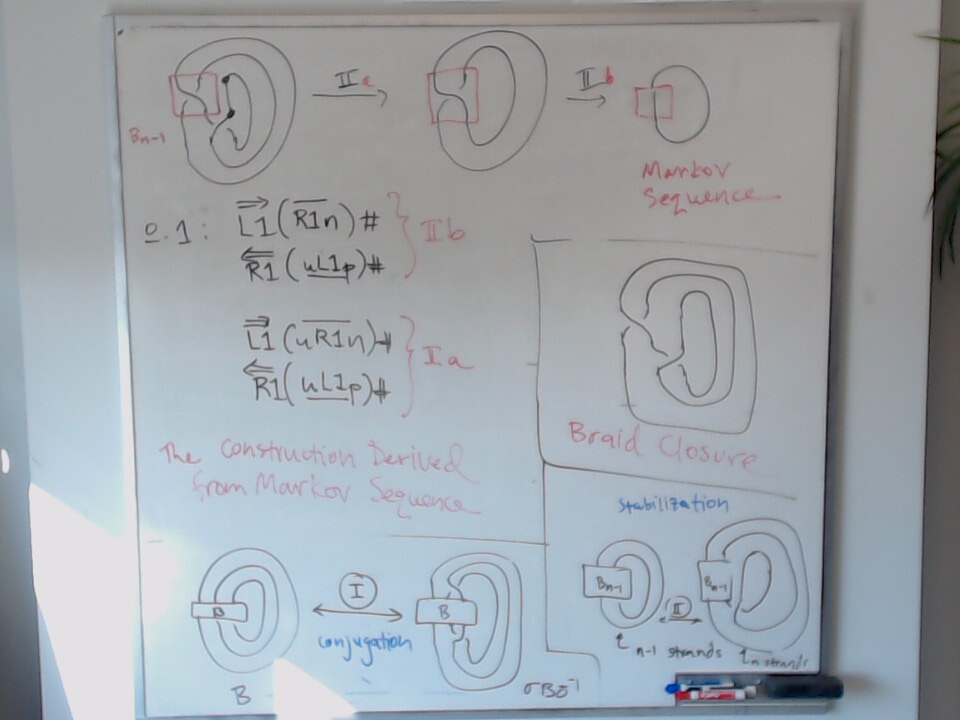
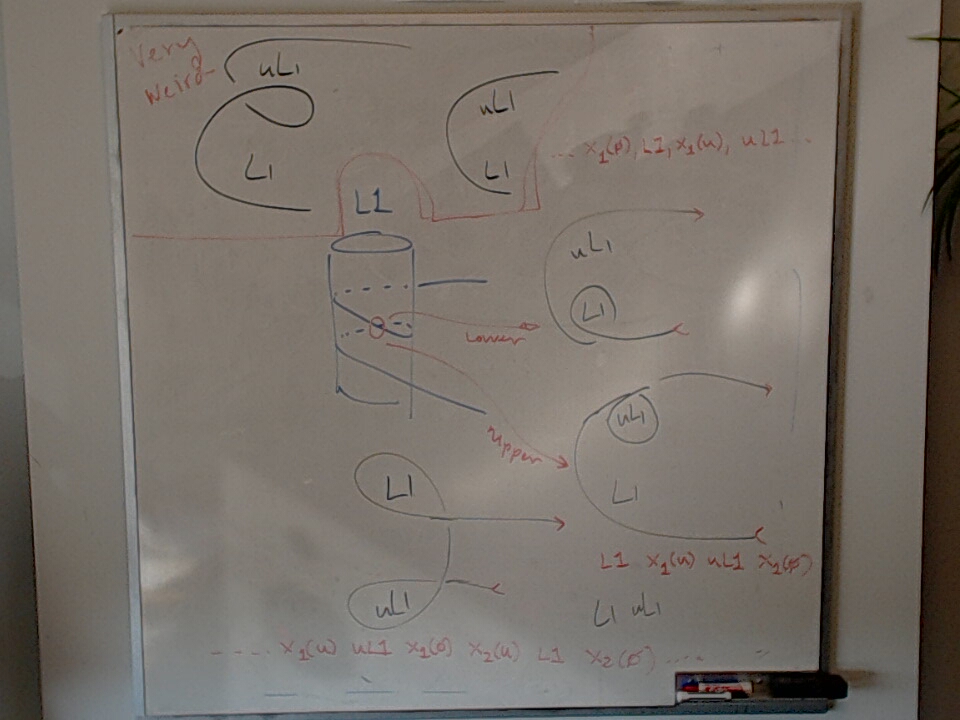

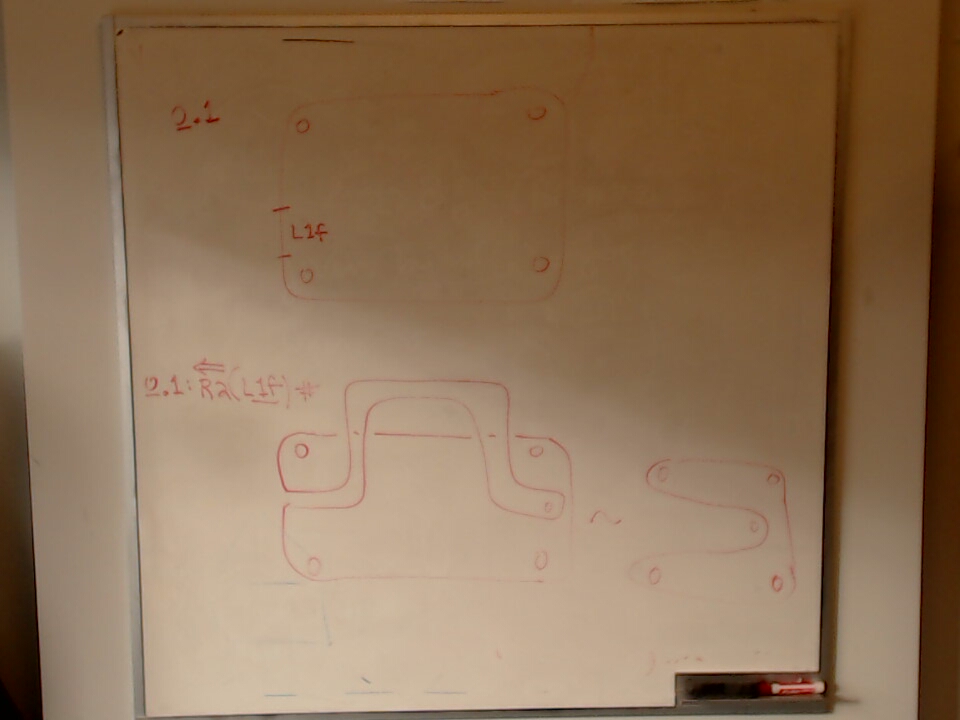




For another discussion of this, see: From a Markov Sequence to a Heart Sequence.



This photo has a sketch of an embedding $\heartsuit_n \leq B_{2n}$.
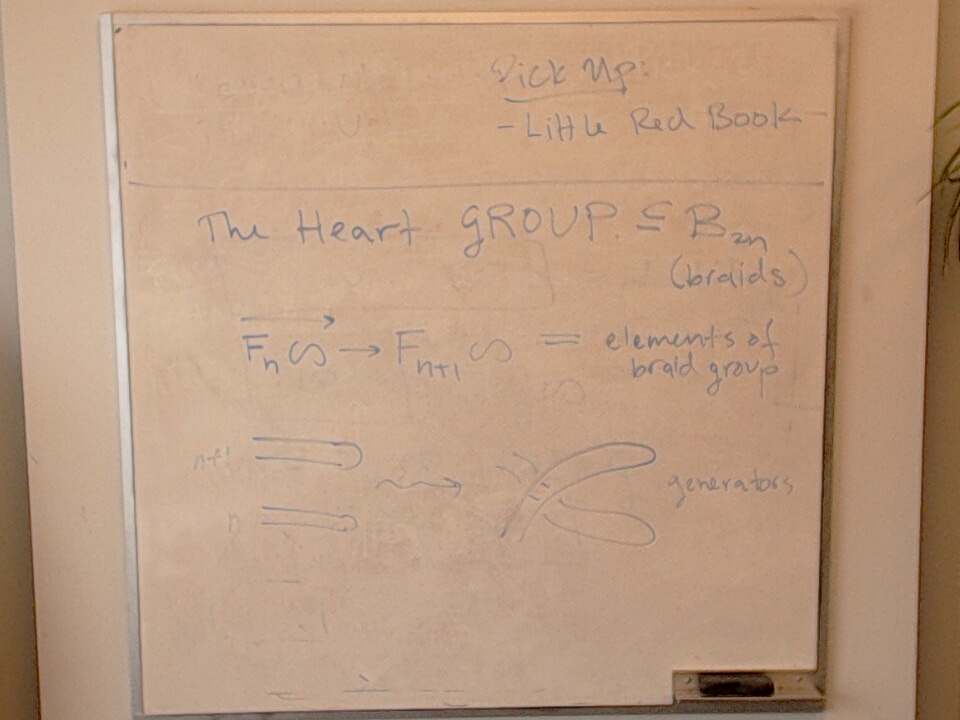
We check a simple lemma leading up to Bessel’s Inequality.
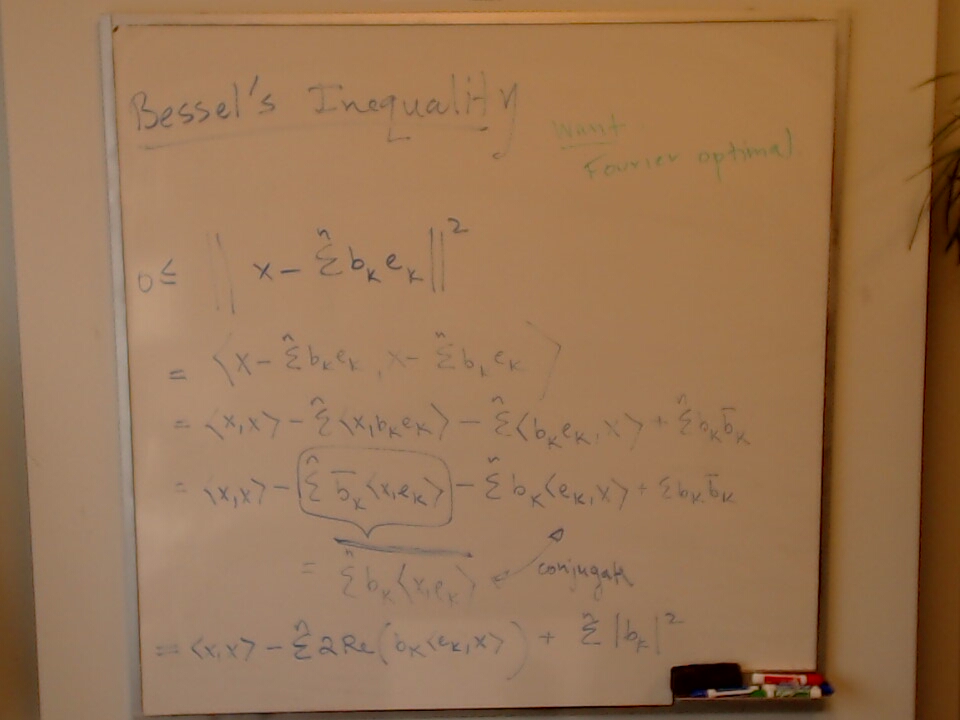


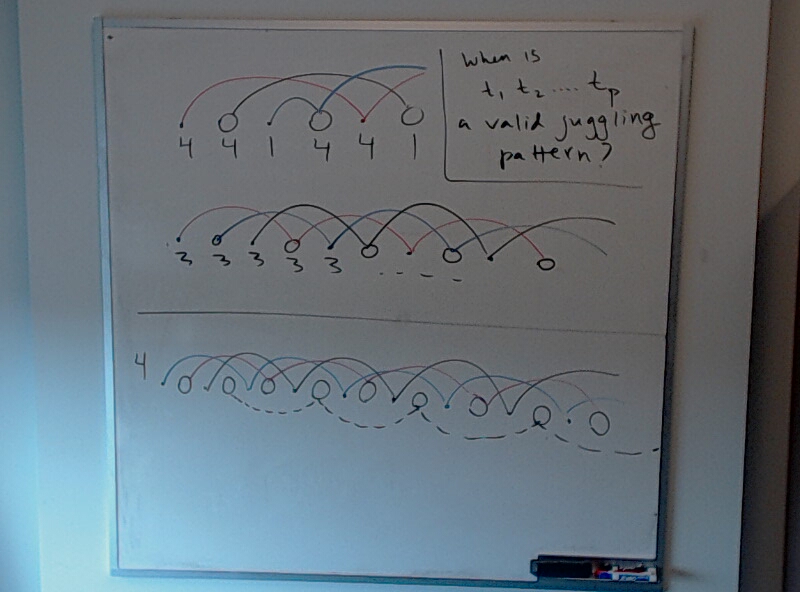
Three loop manipulations are shown. What should we call them?
A quick peek at the braid group $B_3$
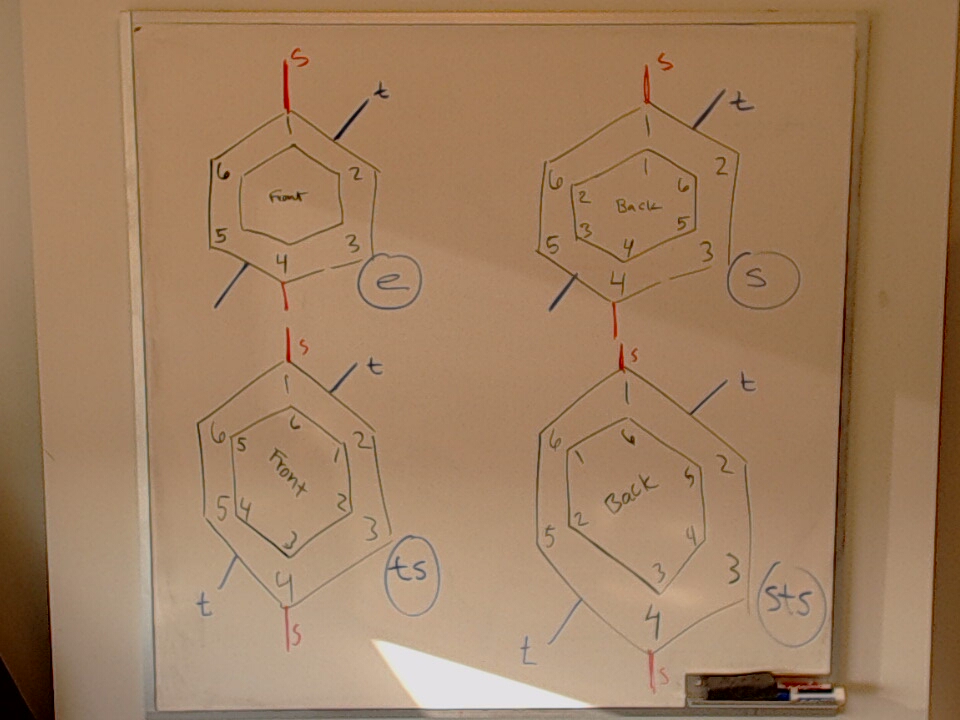
Labelled generators of $H_{n} \subseteq B_{2n}$.















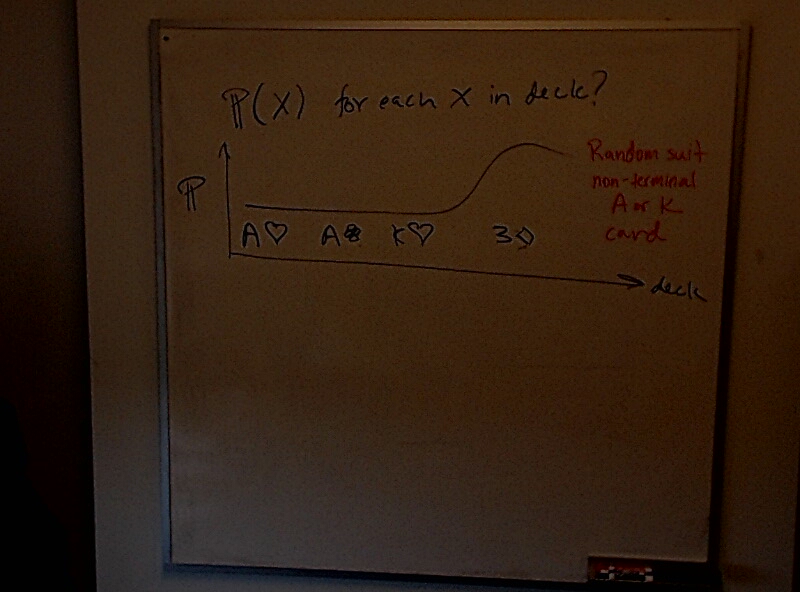
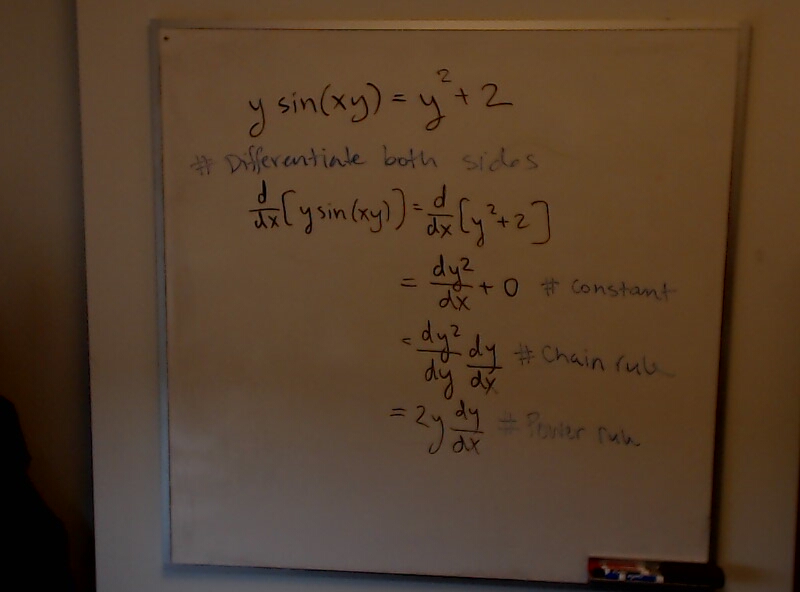
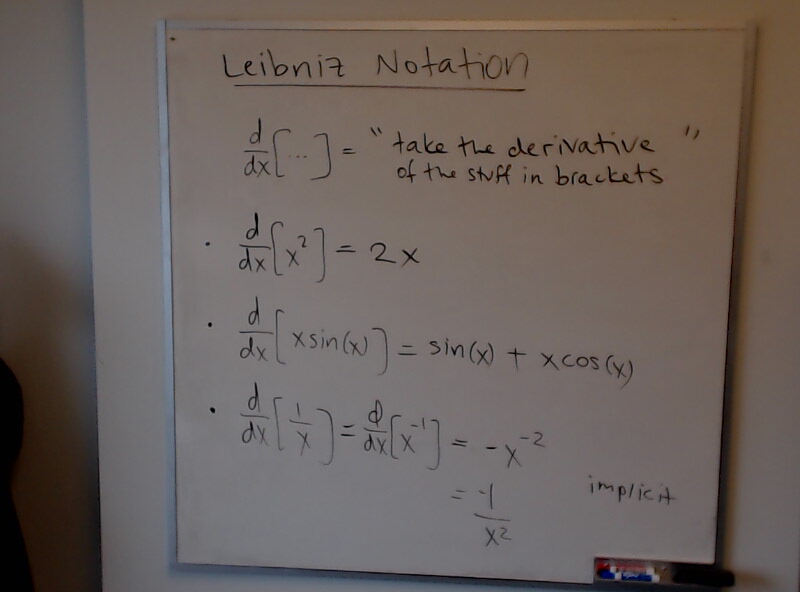









Dave has an amazing summation: $\displaystyle \sum_{n=1}^\infty \frac{n^{13}}{e^{2\pi n} - 1} = \frac{1}{24}$

Home / Now / Blog / Notes / Reading / Office Camera / Tags / Bookmarks / RSS Feeds / Top of Page
Thanks for reading! If you have any comments or questions about the content, please let me know. Anyone can contact me by email.