Gearing up for the next term.
The 8th week of classes. SET Magic and Two Trees Variations.
Fifth week of classes. An anniversary. A new card game.
\[ \begin{array}{cc} \fbox{<3\ <3}\ \overrightarrow{1}\ \underrightarrow{2}\ \overleftarrow{3}\ \overleftarrow{2}\!\downarrow & = \overrightarrow{1}\ \fbox{<3\ <3}\ \underrightarrow{2}\ \overleftarrow{3}\ \overleftarrow{2}\!\downarrow \\ & = \overrightarrow{1}\ \underrightarrow{2}\ \fbox{<2\ <2}\ \overleftarrow{3}\ \overleftarrow{2}\!\downarrow \\ & = \overrightarrow{1}\ \underrightarrow{2}\ \overleftarrow{3}\ \fbox{<3\ <3}\ \overleftarrow{2}\!\downarrow \\ & = \overrightarrow{1}\ \underrightarrow{2}\ \overleftarrow{3}\ \overleftarrow{2}\!\downarrow\ \fbox{<3\ <3}\ \\ \end{array} \]
Third week of classes.
A picture of an elegant string figure position from Nauru.
I collected up some cards for from my cardfile related to a topic.
A pair of string figures from Mary-Rousselière’s Les Jeux de Ficelle Des Arviligjuarmiut.
A string figure formed from two loops.
A picture of a heavily pinned string figure.
Converting a calculation from Storer’s Heart Sequences to the Heart Group
An artist’s book about the relationship between string figures and modernity
A physical example of the complicated braid relation.
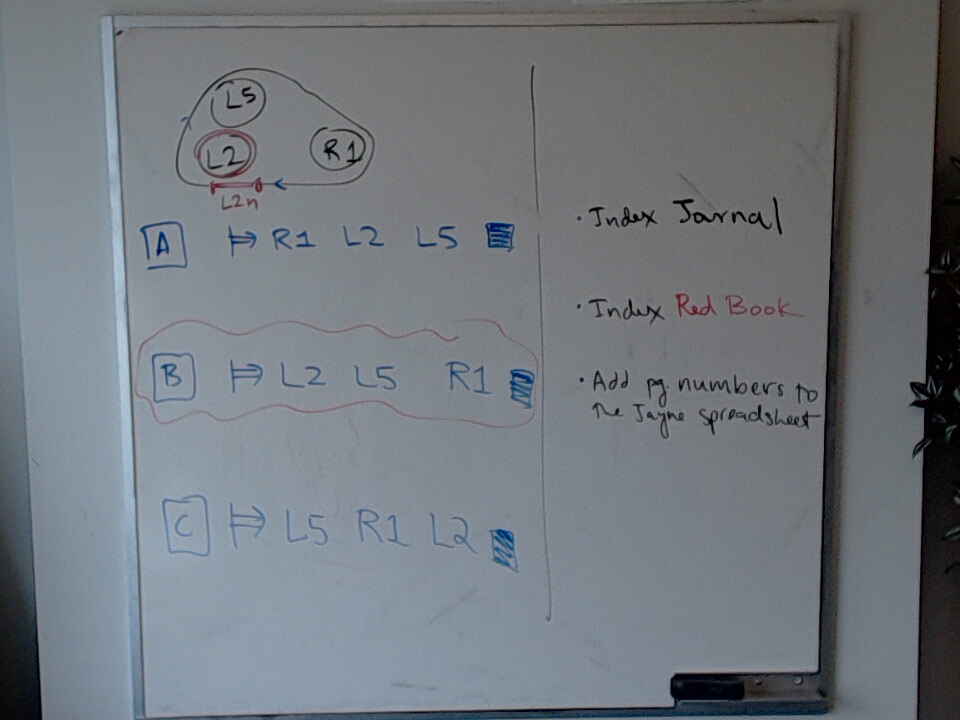
The canonical start of a linear sequence is a point in nearest LFn string. In this simple example, there are three possible linear sequences (with the correct orientation) but only $L2, L5, R1$ has the correct start point.
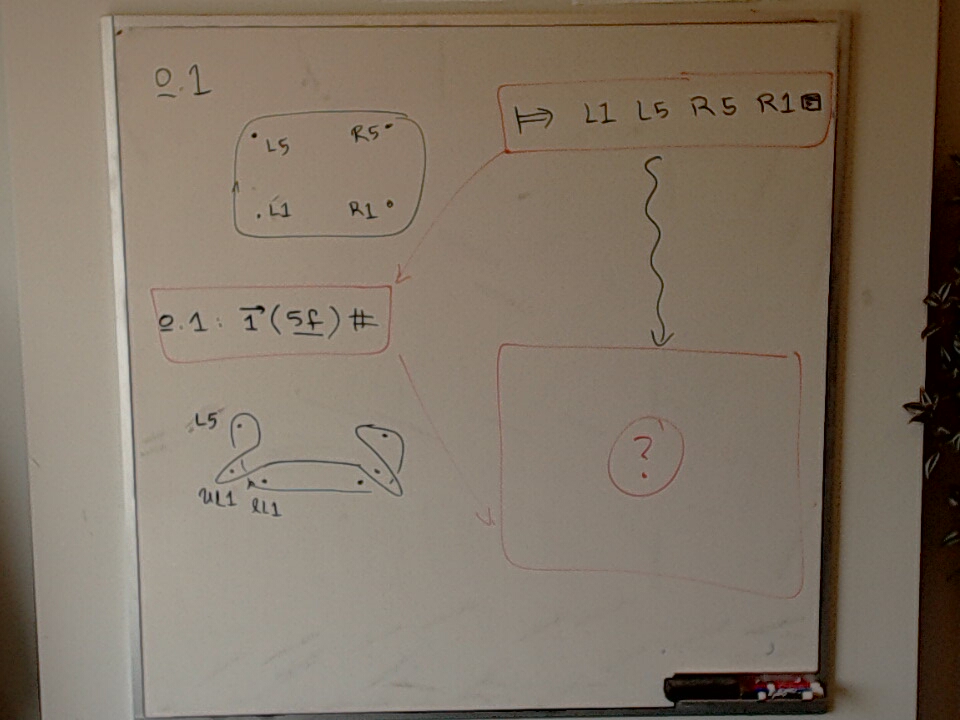
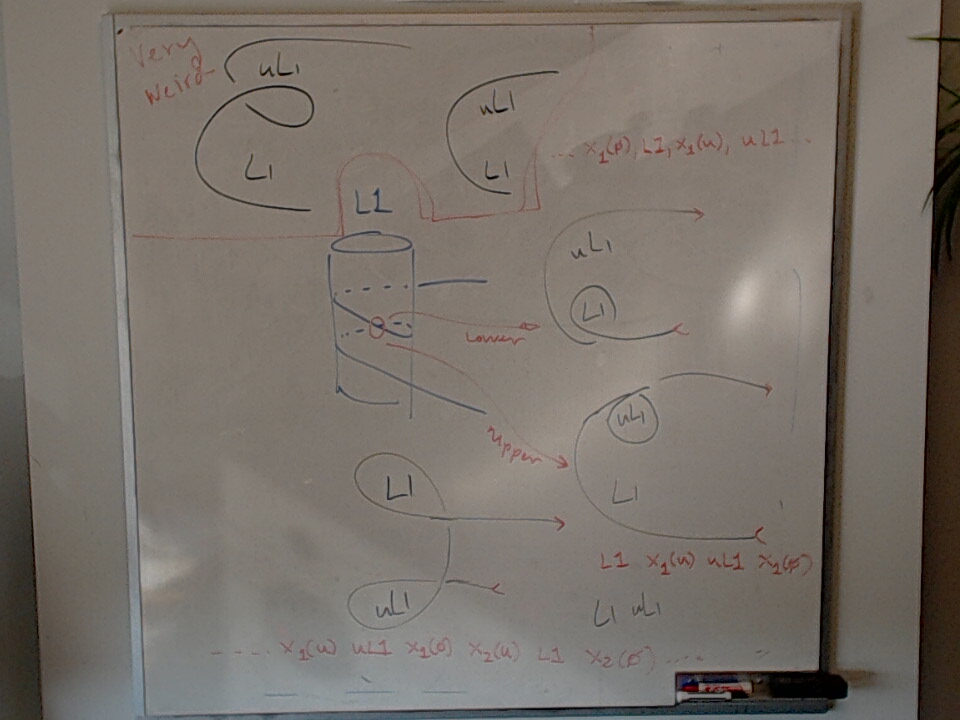
This photo has a sketch of an embedding $\heartsuit_n \leq B_{2n}$.
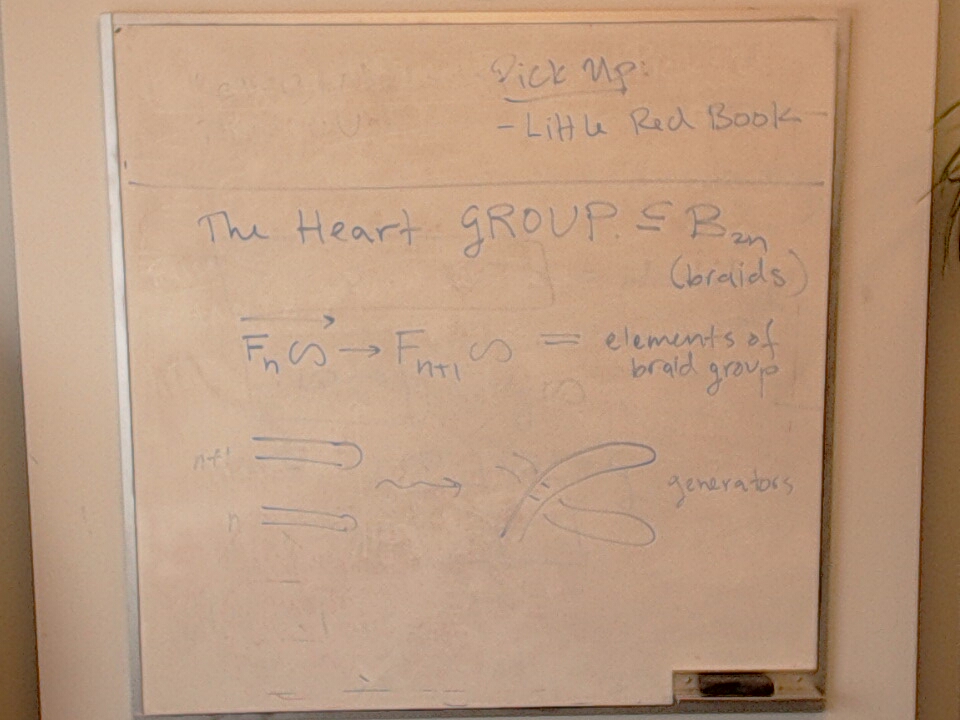
Three loop manipulations are shown. What should we call them?
A quick peek at the braid group $B_3$
A write-up of a question about loop manipulation and braid groups.
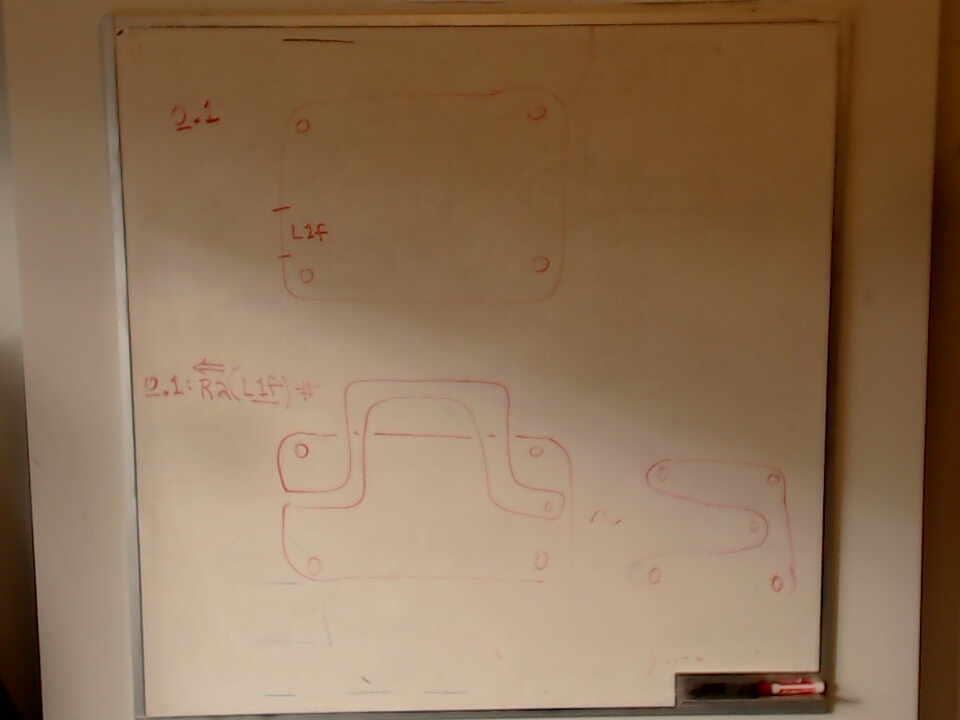
Labelled generators of $H_{n} \subseteq B_{2n}$.
Home / Now / Archive / Office Camera / Bookmarks / Tags / Feeds / Top of Page
Thanks for reading! If you have any comments or questions about the content, please let me know. Anyone can contact me by email.